题目内容
【题目】在锐角△ABC中，角A，B，C的对边分别为a，b，c，满足 
= 
．
（1）求角A的大小；
（2）若a= 
，△ABC的面积S△ABC=3 
，求b+c的值，；
（3）若函数f（x）=2sinxcos（x+ 
），求f（B）的取值范围．
【答案】
（1）解：锐角△ABC中，角A，B，C的对边分别为a，b，c，满足 
= 
，
∴ = 
，
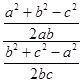整理，得bc=b2+c2﹣a2，
∴cosA= 
= 
= 
，
∴A= 
．
（2）解：∵a= 
，△ABC的面积S△ABC=3 
，A= ，
∴S△ABC= 
=3 ，解得bc=12，
cosA= = 
= ，解得b2+c2=25，
∴（b+c）2=b2+c2+2bc=25+24=49，
∴b+c=7
（3）解：∵f（x）=2sinxcos（x+ 
）
=2sinx（cosxcos ﹣sinxsin ）
= sinxcosx﹣sin2x
= 
sin2x﹣ 
= sin2x+ cos2x﹣
=cos sin2x+sin cos2x﹣
=sin（2x+ ）﹣ ，
∵A= ，∴锐角△ABC中，B∈（0， 
），∴2B+ ∈（ ， 
），
f（B）=sin（2B+ ）﹣ ，
当2B+ = 时，f（B）max=1﹣ = ，
当2B+ = 时，f（B）min=﹣ 
﹣ =﹣ ﹣ ．
∴f（B）的取值范围是（﹣ 
， ）
【解析】（1）利用余弦定理推导出bc=b2+c2﹣a2，从而求出cosA= 
，进而能求出A．（2）由S△ABC= 
=3 
，得bc=12，由余弦定理求出b2+c2=25，从而求出（b+c）2，进而求出b+c的值．（3）由f（x）=2sinxcos（x+ 
）=sin（2x+ 
）﹣ ，A= ，得2B+ ∈（ ， 
），由此能求出f（B）=sin（2B+ ）﹣ 的取值范围．
