题目内容
【题目】如图,在平面直角坐标系xOy中,点P是圆O:x2+y2=1与x轴正半轴的交点,半径OA在x轴的上方,现将半径OA绕原点O逆时针旋转 ![]() 得到半径OB.设∠POA=x(0<x<π),
得到半径OB.设∠POA=x(0<x<π), ![]() .
. 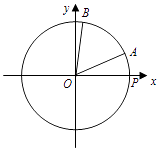
(1)若 ![]() ,求点B的坐标;
,求点B的坐标;
(2)求函数f(x)的最小值,并求此时x的值.
【答案】
(1)解:由题意,因点P是圆O:x2+y2=1与x轴正半轴的交点,又 ![]() ,
,
且半径OA绕原点O逆时针旋转 ![]() 得到半径OB,
得到半径OB,
∴ ![]() .
.
由三角函数的定义,得 ![]() ,
, ![]() ,
,
解得 ![]() ,
, ![]() .
.
∴ 
(2)解:依题意, ![]() ,
, ![]() ,
, ![]() ,
,
由 ![]() ,
,
∴ ![]() ,
,
∴ 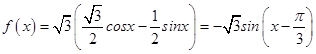 ,
,
∵0<x<π,
则 ![]() ,
,
∴当 ![]() 时,即
时,即 ![]() ,
,
函数f(x)取最小值为 ![]()
【解析】(1)根据三角函数的定义求解即可.(2) ![]() ,求出f(x)的解析式,化简,利用三角函数的性质求解即可.
,求出f(x)的解析式,化简,利用三角函数的性质求解即可.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目