题目内容
已知数列 满足:
满足: ,
,  ,
, ,前
,前 项和为
项和为 的数列
的数列 满足:
满足:

 ,又
,又
 。
。
(1)求数列 的通项公式;
的通项公式;
(2)证明:
 ;
;
【答案】
(1)
(2)先根据通项公式来求解数列的和然后放缩法来得到结论。
【解析】
试题分析:解:(1)由条件得
 ,易知
,易知 ,两边同除以
,两边同除以 得
得
 ,又
,又 ,故
,故


 。 4分
。 4分
(2)因为:
 ,所以
,所以


 ,
6分
,
6分
故只需证 ,
,
由条件







一方面:当 时
时
当 时,
时,


 .11分
.11分
另一方面:当 时,
时, 所以
所以

所以当 时
时 12分
12分
考点:数列的求和
点评:主要是考查了数量积的求和的运用,裂项求和是重要的求和之一,要掌握好。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,则此数列的通项
,则此数列的通项 等于
等于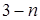 B.
B. C.
C.  D.
D. 
 满足:
满足: .
. ;
; ,求数列
,求数列 的通项公式;
的通项公式; ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.