题目内容
已知函数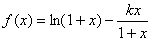 ,
,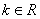 .
.
(1)讨论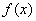 的单调区间;
的单调区间;
(2)当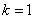 时,求
时,求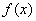 在
在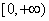 上的最小值,并证明
上的最小值,并证明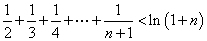 .
.
解:(1)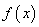 的定义域为
的定义域为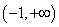 . (1分)
. (1分)
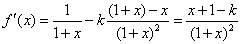 (3分)
(3分)
当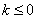 时,
时,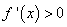 在
在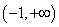 上恒成立,所以
上恒成立,所以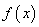 的单调递增区间是
的单调递增区间是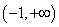 ,无单调递减区间. (5分)
,无单调递减区间. (5分)
当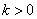 时,由
时,由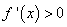 得
得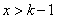 ,由
,由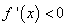 得
得 ,所以
,所以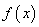 的单调递增区间是
的单调递增区间是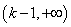 ,单调递减区间是
,单调递减区间是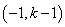 , (7分)
, (7分)
(2)由(1)知,当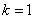 时,
时,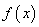 在
在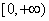 上单调递增,所以
上单调递增,所以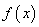 在
在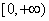 上的最小值为
上的最小值为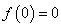 . (9分)
. (9分)
所以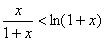 (
(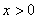 ) (10分)
) (10分)
所以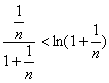 ,即
,即 (
(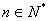 ). (12分)
). (12分)
所以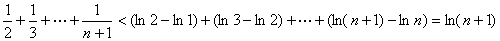

练习册系列答案
相关题目
 ” 的逆否命题是 .
” 的逆否命题是 . 中,若
中,若 ________.
________.
 中,若
中,若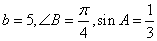 ,则
,则 .
.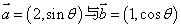 互相平行,其中
互相平行,其中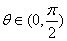 .
.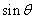 和
和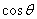 的值;
的值; ,求
,求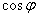 的值.
的值.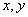 满足约束条件
满足约束条件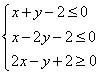 ,若
,若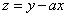 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数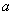 的值为
的值为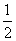 或
或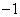 B.2或
B.2或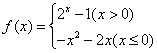 若函数
若函数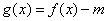 有3个零点,则实数
有3个零点,则实数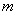 的取值范围是 。
的取值范围是 。 ,实数
,实数 ,则
,则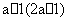 ,则( )
,则( ) 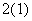 且a≠-1 B.-1<a<0
且a≠-1 B.-1<a<0 D.-1<a<2
D.-1<a<2