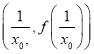题目内容
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上的最大值是
上的最大值是![]() ,求
,求![]() 的值;
的值;
(3)记![]() ,当
,当![]() 时,若对任意
时,若对任意![]() ,总有
,总有![]() 成立,试求
成立,试求![]() 的最大值.
的最大值.
【答案】(1)增区间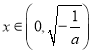 ;减区间
;减区间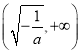 ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数的知识求解;(2)借助题设运用分类整合思想探求;(3)借助题设构造函数,运用导数的有关知识分析探求.
试题解析:
(1)![]() 的定义域是
的定义域是![]() .
.![]() .当
.当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是增函数; 当
上是增函数; 当![]() 时,令
时,令![]() ,则
,则![]() (舍去); 当
(舍去); 当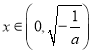 时,
时,![]() ,故
,故![]() 在
在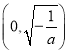 上是增函数;当
上是增函数;当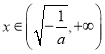 时,
时,![]() ,故
,故![]() 在
在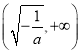 上是减函数.
上是减函数.
(2)①当![]() 时,
时,![]() 在
在![]() 上是增函数; 故在
上是增函数; 故在![]() 上的最大值是
上的最大值是 ![]() ,显然不合题意. ②若
,显然不合题意. ②若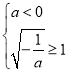 , 即
, 即![]() 时,
时, 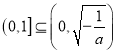 ,则
,则![]() 在
在![]() 上是增函数,故在
上是增函数,故在![]() 上的最大值是
上的最大值是 ![]() ,不合题意,舍去.
,不合题意,舍去.
③ 若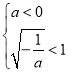 , 即
, 即![]() 时,
时,![]() 在
在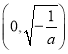 上是增函数 ,在
上是增函数 ,在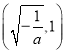 上是减函数,故在
上是减函数,故在![]() 上的最大值是
上的最大值是 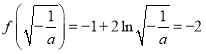 , 解得
, 解得![]() ,符合. 综合①、②、③得:
,符合. 综合①、②、③得: ![]() .
.
(3)![]() , 则
, 则![]() ,当
,当![]() 时,
时,![]() ,故
,故![]() 时,当
时,当![]() 在
在![]() 上是减函数,不妨设
上是减函数,不妨设![]() ,则
,则![]() ,故
,故![]() 等价于
等价于![]() ,即
,即![]() ,记
,记
![]() ,从而
,从而![]() 在
在![]() 上为减函数,由
上为减函数,由![]() 得:
得:
![]() ,故
,故![]() 恒成立,
恒成立,![]() ,又
,又
![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() .故当
.故当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某种产品的年销售量![]() 与该年广告费用支出
与该年广告费用支出![]() 有关,现收集了4组观测数据列于下表:
有关,现收集了4组观测数据列于下表:
| 1 | 4 | 5 | 6 |
| 30 | 40 | 60 | 50 |
现确定以广告费用支出![]() 为解释变量,销售量
为解释变量,销售量![]() 为预报变量对这两个变量进行统计分析.
为预报变量对这两个变量进行统计分析.
(1)已知这两个变量满足线性相关关系,试建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)假如2017年广告费用支出为10万元,请根据你得到的模型,预测该年的销售量![]() .
.
(线性回归方程系数公式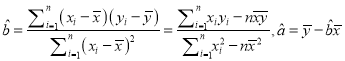 ).
).