题目内容
给出下列四个命题:
①梯形的对角线相等;②对任意实数x,均有 ;
;
③不存在实数x,使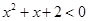 ;④有些三角形不是等边三角形;
;④有些三角形不是等边三角形;
其中真命题的个数为( )
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:①:只有当梯形为等腰梯形的时候,对角线才相等,∴①错误;
②:不等式显然成立,∴②正确;
③: ,∴③正确;
,∴③正确;
④:显然正确,因此真命题的个数为3.
考点:命题与证明.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
在 中,角
中,角 所对应的边分别为
所对应的边分别为 ,则
,则 是
是 的( ).
的( ).
| A.充分必要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.非充分非必要条件 |
已知命题
 ,
, ;命题
;命题
 ,
, ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )
A. | B. | C. | D. |
下列命题中,真命题是( )
| A.?x∈R,ex≤0 |
| B.?x∈R,2x>x2 |
C.a+b=0的充要条件是 =-1 =-1 |
| D.a>1,b>1是ab>1的充分条件 |
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数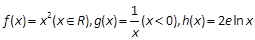 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
设 ,集合
,集合 是奇数集,集合
是奇数集,集合 是偶数集.若命题
是偶数集.若命题 ,则( )
,则( )
A.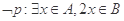 | B. |
C. | D. |
“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分条件 | B.必要条件 |
| C.充分必要条件 | D.既非充分又非必要条件 |
 ;命题
;命题 均是第一象限的角,且
均是第一象限的角,且 ,则
,则 ,下列命题是真命题的是( )
,下列命题是真命题的是( )


