题目内容
如图,PA⊥平面ABC,∠ACB=90°且PA=AC=BC=a,则异面直线PB与AC所成的角的正切值等于 .
【答案】分析:先过B作BD∥AC,且BD=AC得到下底面为矩形,把问题转化为求∠PBD;然后通过PA⊥DB,DB⊥AD证得DB⊥平面PAD,进而求出BD,PA;在RT△PDB中,求出∠PBD的正切值即可.
解答: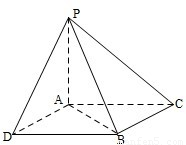 解:过B作BD∥AC,且BD=AC;
解:过B作BD∥AC,且BD=AC;
所以ADBC为矩形
且∠PBD(或其补角)即为所求.
因为PA=AC=BC=a
∴AD=a;BD=a
∵PA⊥平面ABC
∴PD=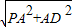 =
=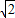 a;
a;
又因为PA⊥DB,DB⊥AD⇒DB⊥平面PAD⇒BD⊥PD.
在RT△PDB中,tan∠PBD=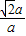 =
=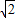 .
.
即异面直线PB与AC所成的角的正切值等于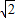 .
.
故答案为: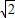 .
.
点评:本题主要考察异面直线及其所成的角.解决本题的关键在于通过过B作BD∥AC,把问题转化为求∠PBD.
解答:
 解:过B作BD∥AC,且BD=AC;
解:过B作BD∥AC,且BD=AC;所以ADBC为矩形
且∠PBD(或其补角)即为所求.
因为PA=AC=BC=a
∴AD=a;BD=a
∵PA⊥平面ABC
∴PD=
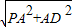 =
=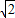 a;
a;又因为PA⊥DB,DB⊥AD⇒DB⊥平面PAD⇒BD⊥PD.
在RT△PDB中,tan∠PBD=
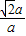 =
=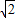 .
.即异面直线PB与AC所成的角的正切值等于
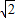 .
.故答案为:
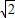 .
.点评:本题主要考察异面直线及其所成的角.解决本题的关键在于通过过B作BD∥AC,把问题转化为求∠PBD.

练习册系列答案
相关题目
 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点. 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 如图,PA⊥平面ABC,AC⊥BC,AB=2,
如图,PA⊥平面ABC,AC⊥BC,AB=2, (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.