题目内容
已知在函数![]() 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为![]()
(1)求m、n的值;
(2)是否存在最小的正整数k,使得不等式![]() 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
(3)求证:![]()
解:(1)![]() 依题意,
依题意,
得![]()
∴![]()
∴![]()
(2)令![]()
当![]() 在此区间为增函数
在此区间为增函数
当![]() 在此区间为减函数
在此区间为减函数
当![]() 在此区间为增函数
在此区间为增函数
![]() 处取得极大值
处取得极大值
又![]()
因此,当![]()
要使得不等式![]()
所以,存在最小的正整数k=2007,使得不等式![]() 恒成立。
恒成立。
(3)(方法一)![]()
![]()
![]()
![]()
又∵![]()
∴![]()
∴![]()
![]()
综上可得
![]()
(方法2)由(2)知,函数![]()
上是减函数,在[![]() ,1]上是增函数
,1]上是增函数
又![]()
所以,当![]() 时,-
时,-![]()
![]()
![]()
![]()
又t>0,
![]() ,且函数
,且函数![]() 上是增函数,
上是增函数,
![]()
综上可得
![]() …
…

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
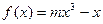 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为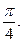
 (2)是否存在最小的正整数k,使得不等式
(2)是否存在最小的正整数k,使得不等式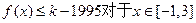 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由; )求证:
)求证: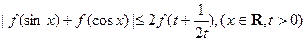 .
.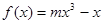 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为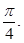
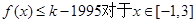 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;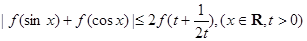 .
.