题目内容
如图,在三棱柱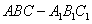 中,
中,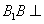 平面
平面
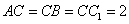 ,
,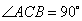 ,
, 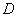 ,
,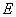 分别是
分别是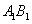 ,
,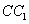 的中点.
的中点.
(Ⅰ)求证: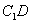 ∥平面
∥平面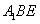 ;
;
(Ⅱ)求证:平面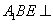 平面
平面 ;
;
(Ⅲ)求直线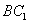 与平面
与平面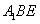 所成角的正弦值.
所成角的正弦值.
 |
证明:(Ⅰ)取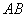 的中点
的中点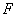 ,连结
,连结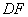 ,交
,交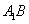 于点
于点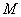 ,可知
,可知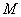 为
为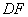 中点,
中点,
连结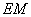 ,易知四边形
,易知四边形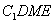 为平行四边形,
为平行四边形,
所以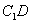 ∥
∥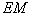 .
.
又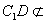 平面
平面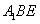 ,
,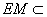 平面
平面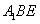 ,
,
所以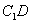 ∥平面
∥平面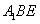 .
.
证明:(Ⅱ)因为 ,且
,且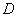 是
是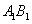 的中点,
的中点,
所以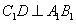 .
.
因为 平面
平面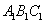 ,所以
,所以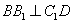 .
.
所以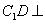 平面
平面 .
.
又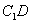 ∥
∥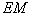 ,所以
,所以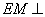 平面
平面 .
.
又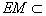 平面
平面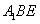 ,
,
所以平面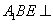 平面
平面 .
.
解:(Ⅲ)如图建立空间直角坐标系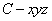 ,
,
则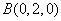 ,
,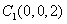 ,
, 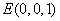 ,
,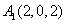 .
.
|

练习册系列答案
相关题目
2014年一轮又一轮的寒潮席卷全国.某商场为了了解某品牌羽绒服的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气
温,数据如下表:
月平均气温x(℃) | 17 | 13 | 8 | 2 |
月销售量y(件) | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程=bx+a中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月羽绒服的销售量约为________件.
 ,若存在实数
,若存在实数 ,满足
,满足 ,其中
,其中 ,则
,则 取值范围是 .
取值范围是 . 中,
中,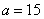 ,
,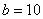 ,
,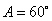 ,则
,则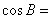
 (B)
(B)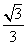
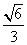 (D)
(D)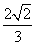
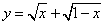 的最大值为 .
的最大值为 .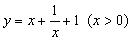 的最小值为
的最小值为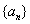 满足
满足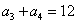 ,
, 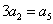 ,那么
,那么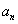 =___________.
=___________.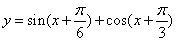 的最大值是
的最大值是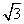 (D)
(D)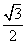
 是抛物线
是抛物线 :
: 的焦点,则
的焦点,则 _______.
_______.