题目内容
若cosθ=- ,θ∈(π,2π),则tan
,θ∈(π,2π),则tan =( )
=( )A.-2
B.-

C.-

D.-
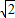
【答案】分析:利用同角三角函数的基本关系,由cosθ及θ的范围求出sinθ,从而求出tanθ,再由二倍角公式求出tan .
.
解答:解:∵cosθ=- ,θ∈(π,2π),
,θ∈(π,2π),
∴sinθ=-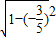 =-
=-
∴tanθ=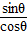 =
=
tanθ=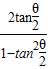 =
=
解得;tan =-2或
=-2或
∵θ∈(π,2π),
 ∈(
∈(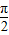 ,π)
,π)
∴tan =-2
=-2
故选;A.
点评:此题考查了同角三角函数的基本关系以及二倍角公式,熟练掌握公式是解题的关键.
 .
.解答:解:∵cosθ=-
 ,θ∈(π,2π),
,θ∈(π,2π),∴sinθ=-
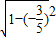 =-
=-
∴tanθ=
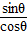 =
=
tanθ=
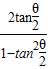 =
=
解得;tan
 =-2或
=-2或
∵θ∈(π,2π),
 ∈(
∈(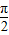 ,π)
,π)∴tan
 =-2
=-2故选;A.
点评:此题考查了同角三角函数的基本关系以及二倍角公式,熟练掌握公式是解题的关键.

练习册系列答案
相关题目
若cos
=
,sin
=-
,则角θ的终边一定落在直线( )上.
| θ |
| 2 |
| 3 |
| 5 |
| θ |
| 2 |
| 4 |
| 5 |
| A、7x+24y=0 |
| B、7x-24y=0 |
| C、24x+7y=0 |
| D、24x-7y=0 |
若cos(2π-α)=
,α∈(-
,0),则cos(α-
)=( )
| 1 |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、±
|