题目内容
已知函数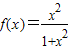 .
.(1)求f(2)与
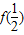 ,f(3)与
,f(3)与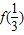 ;
;(2)由(1)中求得结果,你能发现f(x)与
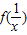 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;(3)求
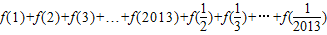 的值.
的值.
【答案】分析:(1)由f(x)=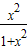 即可求得f(2),f(
即可求得f(2),f( ),f(3),f(
),f(3),f( );
);
(2)易证f(x)+f(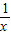 )=1,从而可求f(1)+f(2)+f(3)+…+f(2013)+f(
)=1,从而可求f(1)+f(2)+f(3)+…+f(2013)+f( )+f(
)+f( )+…+f(
)+…+f(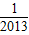 )的值.
)的值.
解答:解:(1)f(2)= ,f(
,f( )=
)= …1分
…1分
f(3)=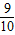 ,f(
,f( )=
)=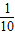 …2分
…2分
(2)f(x)+f(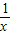 )=1…5分
)=1…5分
证:f(x)+f(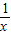 )=
)=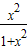 +
+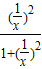 =
=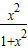 +
+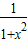 =1…8分
=1…8分
(3)f(1)+f(2)+f(3)+…+f(2013)+f( )+f(
)+f( )+…+f(
)+…+f(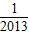 )
)
=f(1)+[f(2)+f( )]+[f(3)+f(
)]+[f(3)+f( )]+…+[f(2013)+f(
)]+…+[f(2013)+f(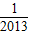 )]
)]
= +2012
+2012
=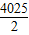 …12分
…12分
点评:本题考查函数的值,考查数列的求和,求得f(x)+f(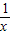 )=1是关键,考查分析、转化与运算能力,属于中档题.
)=1是关键,考查分析、转化与运算能力,属于中档题.
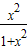 即可求得f(2),f(
即可求得f(2),f( ),f(3),f(
),f(3),f( );
);(2)易证f(x)+f(
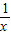 )=1,从而可求f(1)+f(2)+f(3)+…+f(2013)+f(
)=1,从而可求f(1)+f(2)+f(3)+…+f(2013)+f( )+f(
)+f( )+…+f(
)+…+f(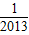 )的值.
)的值.解答:解:(1)f(2)=
 ,f(
,f( )=
)= …1分
…1分f(3)=
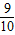 ,f(
,f( )=
)=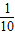 …2分
…2分(2)f(x)+f(
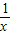 )=1…5分
)=1…5分证:f(x)+f(
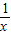 )=
)=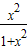 +
+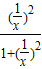 =
=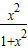 +
+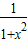 =1…8分
=1…8分(3)f(1)+f(2)+f(3)+…+f(2013)+f(
 )+f(
)+f( )+…+f(
)+…+f(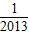 )
)=f(1)+[f(2)+f(
 )]+[f(3)+f(
)]+[f(3)+f( )]+…+[f(2013)+f(
)]+…+[f(2013)+f(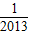 )]
)]=
 +2012
+2012=
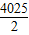 …12分
…12分点评:本题考查函数的值,考查数列的求和,求得f(x)+f(
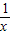 )=1是关键,考查分析、转化与运算能力,属于中档题.
)=1是关键,考查分析、转化与运算能力,属于中档题. 
练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.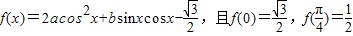 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.