题目内容
【题目】如图,已知斜三棱柱![]() 中,
中,![]() ,
,![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,且
,且![]() .
.
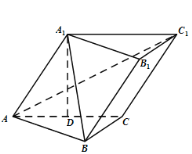
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的平面角为
的平面角为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)见解析(2)![]() (3)不存在点
(3)不存在点![]() 满足要求.见解析
满足要求.见解析
【解析】
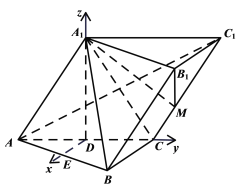
(1)作![]() 交
交![]() 于点
于点![]() ,分别以
,分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,利用空间向量法证明
轴建立空间直角坐标系,利用空间向量法证明![]() ;
;
(2)利用(1)中所建坐标系,求出直线的方向向量和平面![]() 的一个法向量,则两向量的夹角的余弦值的绝对值即为线与面的夹角的正弦值;
的一个法向量,则两向量的夹角的余弦值的绝对值即为线与面的夹角的正弦值;
(3)假设存在设![]() (
(![]() ),求出平面
),求出平面![]() 的一个法向量,根据
的一个法向量,根据![]() ,即可求出
,即可求出![]() 的值,即可得证.
的值,即可得证.
证明:(1)作![]() 交
交![]() 于点
于点![]() ,分别以
,分别以![]() 所在直线为
所在直线为![]() 轴建系
轴建系
![]() 所以,
所以,![]()
![]() ,所以
,所以![]()
(2)因为![]() ,所以面
,所以面![]() 的一个法向量为
的一个法向量为![]()
因为![]() ,所以
,所以![]() ,
,![]()
![]()
设线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]()
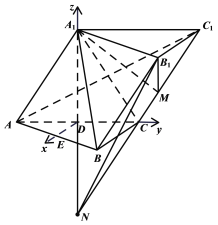
(3)不存在,设![]() ,(
,(![]() )
)
![]() ,
,![]()
设面![]() 的一个法向量为
的一个法向量为![]()
有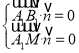
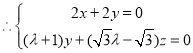
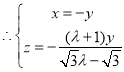
![]()
![]() ,得
,得![]()
所以不存在点![]() 满足要求.
满足要求.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分高于省一本线分值对比表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
录取平均分高于省一本线分值 | 28 | 34 | 41 | 47 | 50 |
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)假设2020年该省一本线为520分,利用(1)中求出的回归方程预测2020年该大学录取平均分.
参考公式: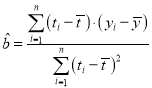 ,
,![]()