题目内容
(本小题12分)如图,  、
、 分别是正四棱柱
分别是正四棱柱 上、下底面的中
上、下底面的中
心, 是
是 的中点,
的中点, .
.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ当 取何值时,
取何值时, 在平面
在平面 内的射影恰好为
内的射影恰好为 的重心?
的重心?

【答案】
(Ⅱ)当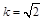 时,
时,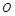 在平面
在平面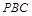 内的射影恰好为
内的射影恰好为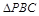 的重心.
的重心.
(Ⅱ)解 由(Ⅰ)知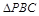 的重心
的重心 为
为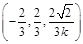 ,则
,则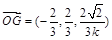 ,
,
(Ⅰ)证明 见解析;
|
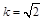 时,
时,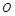 在平面
在平面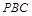 内的射影恰好为
内的射影恰好为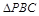 的重心.
的重心.
【解析】本题是中档题,考查空间向量求直线与平面平行,法向量的求法,直线与平面所成的角,考查计算能力.
(1)以点O为原点,直线OA、OB、OP所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,不妨设AB=2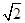 ,然后利用平面向量基本定理来证明线面平行。
,然后利用平面向量基本定理来证明线面平行。
(2)先由(Ⅰ)知△PBC的重心G坐标,然后利用利用数量积垂直关系为0,得到参数k的值。
以点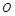 为原点,直线
为原点,直线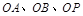 所在直线分别为
所在直线分别为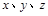 轴,
轴,
建立如图所示的空间直角坐标系,

不妨设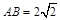 ,
,
则得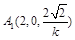 、
、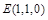 、
、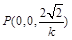 、
、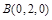 、
、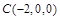
(Ⅰ)证明 由上得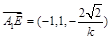 、
、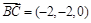 、
、
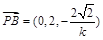 ,设
,设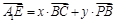 得
得
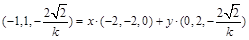
解得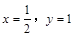 , ∴
, ∴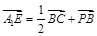
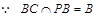 ,
, ∴
∴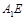 ∥平面
∥平面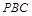
|
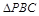 的重心
的重心 为
为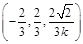 ,则
,则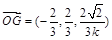 ,
,
若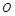 在平面
在平面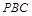 内的射影恰好为
内的射影恰好为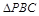 的重心,则有
的重心,则有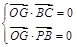 ,解得
,解得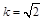
∴当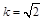 时,
时,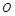 在平面
在平面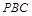 内的射影恰好为
内的射影恰好为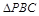 的重心.
的重心.

练习册系列答案
相关题目
 中,AC=BC, AC⊥BC,点D是A1B1中点.
中,AC=BC, AC⊥BC,点D是A1B1中点.  ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.
 中,
中, 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点. 与底面
与底面 平面
平面 ;
; 的余弦值.
的余弦值. 
 中,底面
中,底面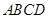 是正方形,
是正方形, ,
,  底面
底面 分别在
分别在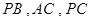 上,且
上,且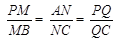
 ∥平面
∥平面 .
. 与平面面
与平面面
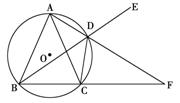

 平面BCD;
平面BCD;