题目内容
2.不等式|x-3|+|x-2|≥3的解集是( )| A. | {x|x≥3或x≤1} | B. | {x|x≥4或x≤2} | C. | {x|x≥2或x≤1} | D. | {x|x≥4或x≤1}. |
分析 把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
解答 解:不等式|x-3|+|x-2|≥3,等价于 $\left\{\begin{array}{l}{x<2}\\{3-x+2-x≥3}\end{array}\right.$①,或$\left\{\begin{array}{l}{2≤x≤3}\\{3-x+x-2≥3}\end{array}\right.$②,或$\left\{\begin{array}{l}{x>3}\\{x-3+x-2≥3}\end{array}\right.$③.
解①求得x≤1,解②求得x∈∅,解③求得x≥4,
综上可得,不等式|x-3|+|x-2|≥3的解集是{x|x≥4或x≤1},
故选:D.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,属于基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
7.已知抛物线y2=2px(p>0)的准线经过点(-1,4),过抛物线的焦点F且与x轴垂直的直线交该抛物线于M、N两点,则|MN|=( )
| A. | 4 | B. | $2\sqrt{3}$ | C. | 2 | D. | 1 |
10.设△ABC的三个内角A,B,C的对边分别为a,b,c满足b2=ac且sinAsinC=$\frac{3}{4}$,则角B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,求此点取自黑色部分的概率.
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,求此点取自黑色部分的概率.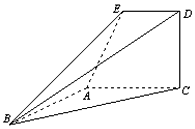 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.