Question

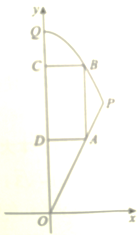
【题目】如图，曲边三角形中，线段是直线的一部分，曲线段是抛物线的一部分.矩形的顶点分别在线段，曲线段和轴上.设点，记矩形的面积为.

（Ⅰ）求函数的解析式并指明定义域；

（Ⅱ）求函数的最大值.

【答案】(Ⅰ) 定义域为;(Ⅱ) 在时，取得最大值.

【解析】试题分析：( I )根据点在直线上，在抛物线上，结合图形，可得点，从而可得函数的解析式，联立直线与抛物线的方程，即可求得定义域；（II）对函数求导，利用导数研究函数的单调性，从而可求得函数的最大值.

试题解析：( I )令，

解得 （舍）

因为点

所以 ，

其定义域为

（II）因为

令，得，（舍）

所以的变化情况如下表

		0
		极大

因为是函数在上的唯一的一个极大值，

所以在时，函数取得最大值.

点睛：利用导数解答函数最值的一般步骤：第一步：利用或求单调区间；第二步：解得两个根；第三步：比较两根同区间端点的大小；第四步：求极值；第五步：比较极值同端点值的大小．

【题型】解答题
【结束】
16

【题目】在各项均为正数的数列中， 且.

（Ⅰ）当时，求的值；

（Ⅱ）求证：当时，.

Answer 1

【答案】(Ⅰ)见解析；（Ⅱ）见解析.

【解析】试题分析：（Ⅰ）根据及，可求得的值，同理即可求得的值；（Ⅱ）利用分析法，要证，只需证 ，即证，然后结合均值不等式即可证明.

试题解析：（Ⅰ）因为，

所以，

所以，

解得，

同理解得.

（Ⅱ）证明：要证 时，，

只需证 ，

只需证 ，只需证 .

只需证 ，

只需证 ，

根据均值定理，

所以原命题成立.