题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点
,点![]() 和点
和点![]() 都在椭圆
都在椭圆![]() 上,直线
上,直线![]() 交x轴于点M.
交x轴于点M.
(1)(Ⅰ)求椭圆C的方程,并求点M的坐标(用![]() ,
,![]() 表示);
表示);
(2)(Ⅱ)设![]() 为原点,点
为原点,点![]() 与点
与点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 交X轴于点N.问:Y轴上是否存在点Q,使得
交X轴于点N.问:Y轴上是否存在点Q,使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】
(1)
M (![]() , 0 )
, 0 )
(2)
存在点 Q ( 0 , ± ![]() ) 使得 ∠ O Q M = ∠ O N Q .
) 使得 ∠ O Q M = ∠ O N Q .
【解析】(I)由于椭圆![]() :
:![]() 过点
过点![]() 且离心率为
且离心率为![]() ,
,![]() ,
,![]() ,椭圆C的方程为
,椭圆C的方程为![]() ,因为
,因为![]()
![]() 直线PA的方程为
直线PA的方程为![]() ,令
,令![]() ,所以
,所以![]() ;
;
(Ⅱ)因为![]()
![]() ,直线PB的方程为:
,直线PB的方程为:![]() ,直线PB与x轴交于点N,令
,直线PB与x轴交于点N,令![]() ,则
,则![]() .
.
设![]()
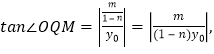
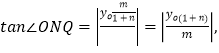 因为
因为![]() 所以
所以![]() ,则
,则![]() ,所以
,所以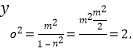 (注:点
(注:点![]() 在椭圆C上,
在椭圆C上,![]() ),则
),则![]() ,存在点
,存在点![]() 使得
使得![]() .
.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目