题目内容
(本题满分16分)对于数列 ,若存在常数M>0,对任意
,若存在常数M>0,对任意 ,恒有
,恒有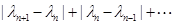
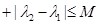 ,则称数列
,则称数列 为
为 数列.
数列.
求证:⑴设 是数列
是数列 的前n项和,若
的前n项和,若 是
是 数列,则
数列,则 也是
也是 数列.
数列.
⑵若数列 都是
都是 数列,则
数列,则 也是
也是 数列.
数列.
 ,若存在常数M>0,对任意
,若存在常数M>0,对任意 ,恒有
,恒有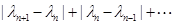
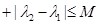 ,则称数列
,则称数列 为
为 数列.
数列. 求证:⑴设
 是数列
是数列 的前n项和,若
的前n项和,若 是
是 数列,则
数列,则 也是
也是 数列.
数列.⑵若数列
 都是
都是 数列,则
数列,则 也是
也是 数列.
数列.证明:(1)∵{Sn}为 数列,∴存在M>0, 使
数列,∴存在M>0, 使
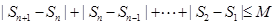
∴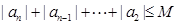 ,又
,又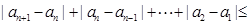
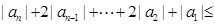
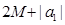 . ∴{an}也是
. ∴{an}也是 数列.
数列.
(2) ∵数列{an}{bn}都是 数列,∴存在M, M'使得:
数列,∴存在M, M'使得:
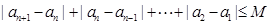 ,
,
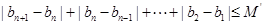 对任意
对任意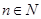 都成立.
都成立.
考虑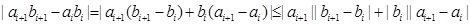
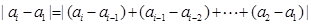
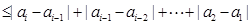
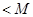 ∴
∴
同理,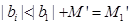
∴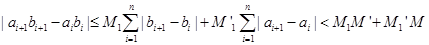
∴{anbn}也是 数列.
数列.
 数列,∴存在M>0, 使
数列,∴存在M>0, 使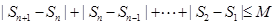
∴
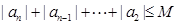 ,又
,又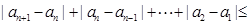
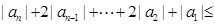
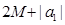 . ∴{an}也是
. ∴{an}也是 数列.
数列. (2) ∵数列{an}{bn}都是
 数列,∴存在M, M'使得:
数列,∴存在M, M'使得: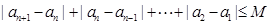 ,
,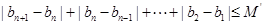 对任意
对任意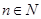 都成立.
都成立.考虑
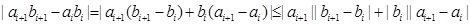
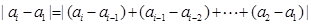
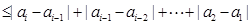
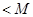 ∴
∴
同理,
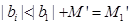
∴
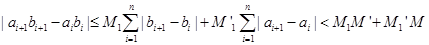
∴{anbn}也是
 数列.
数列.略

练习册系列答案
相关题目
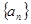
 满足
满足 ,且
,且 ,若数列的前2011项之和为2012,则前2012项的和等于( )
,若数列的前2011项之和为2012,则前2012项的和等于( )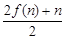 (n∈N*)且f(1)=2,则f(20)为
(n∈N*)且f(1)=2,则f(20)为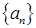 的通项公式为
的通项公式为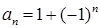 ,则
,则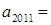 ;
;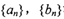 满足
满足 ,则
,则 =
=



 中,
中, ,
, ,则
,则 的值为( )
的值为( )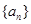 满足:
满足: ,则
,则 ■
■ 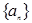 满足
满足 ,
, ,那么
,那么 的值是
的值是 满足:
满足: ,定义使
,定义使
 叫做企盼数,则区间
叫做企盼数,则区间 内所有的企盼数的和为 .
内所有的企盼数的和为 . 