题目内容
已知函数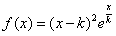 。
。
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若对于任意的x∈(0,+∞),都有f(x)≤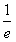 ,求k的取值范围。
,求k的取值范围。
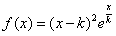 。
。 (Ⅰ)求f(x)的单调区间;
(Ⅱ)若对于任意的x∈(0,+∞),都有f(x)≤
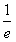 ,求k的取值范围。
,求k的取值范围。 解:(Ⅰ)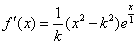 ,
,
令f′(0)=0,得x=±k,
当k>0时,f(x)与f′(x)的情况如下:
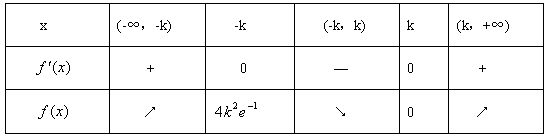
所以,f(x)的单调递减区间是(-∞,-k)和(k,+∞);单调减区间是(-k,k);
当k<0时,f(x)与f′(x)的情况如下:
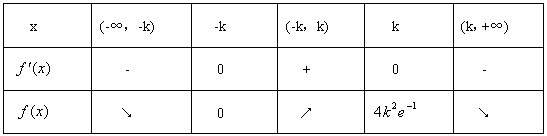
所以,f(x)的单调递减区间是(-∞,-k)和(k,+∞);单调增区间是(-k,k);
(Ⅱ)当k>0时,因为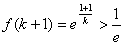 ,所以不会有
,所以不会有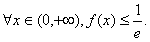 ;
;
当k<0时,由(Ⅰ)知f(x)在(0,+∞)上的最大值是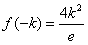 ,
,
所以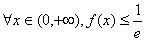 等价于
等价于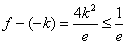 ,
,
解得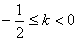 ,
,
故当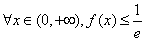 时,k的取值范围是
时,k的取值范围是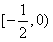 。
。
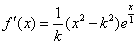 ,
,令f′(0)=0,得x=±k,
当k>0时,f(x)与f′(x)的情况如下:

所以,f(x)的单调递减区间是(-∞,-k)和(k,+∞);单调减区间是(-k,k);
当k<0时,f(x)与f′(x)的情况如下:

所以,f(x)的单调递减区间是(-∞,-k)和(k,+∞);单调增区间是(-k,k);
(Ⅱ)当k>0时,因为
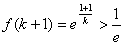 ,所以不会有
,所以不会有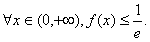 ;
;当k<0时,由(Ⅰ)知f(x)在(0,+∞)上的最大值是
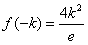 ,
,所以
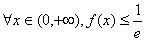 等价于
等价于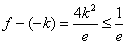 ,
,解得
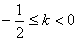 ,
,故当
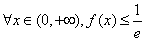 时,k的取值范围是
时,k的取值范围是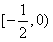 。
。 
练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.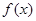 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求