题目内容
函数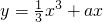
在区间[0，1]上是增函数，则a的取值范围为
- A.a＞0
- B.a＜0
- C.a≥0
- D.a≤0
C
分析：由函数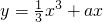在[0，1]上是增函数，转化成y′=x2+a≥0在[0，1]内恒成立，利用参数分离法即可求出a的范围．
解答：∵由函数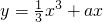在[0，1]上是增函数，
∴y′=x2+a≥0在[0，1]内恒成立．
即 a≥-x2在[0，1]内恒成立．
∵t=-x2在[0，1]上的最大值为 0，
∴a的取值范围为：a≥0．
故选C．
点评：此题主要考查利用导函数的正负判断原函数的单调性，利用参数分离法解决恒成立问题，属于基础题．
分析：由函数
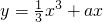在[0，1]上是增函数，转化成y′=x2+a≥0在[0，1]内恒成立，利用参数分离法即可求出a的范围．解答：∵由函数
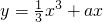在[0，1]上是增函数，∴y′=x2+a≥0在[0，1]内恒成立．
即 a≥-x2在[0，1]内恒成立．
∵t=-x2在[0，1]上的最大值为 0，
∴a的取值范围为：a≥0．
故选C．
点评：此题主要考查利用导函数的正负判断原函数的单调性，利用参数分离法解决恒成立问题，属于基础题．
练习册系列答案
相关题目
)和(
,1)内分别( )
（I）求曲线
处的切线方程； （Ⅱ）求证函数
在区间[0，1]上存在唯一的极值点，并用二分法求函数取得极值时相应x的近似值（误差不超过0.2）；（参考数据e≈2.7，
≈1.6，e0.3≈1.3）
试求实数
的取值范围。
在区间[0，1]上有最小值－2，求
的值．
在区间[0，1]上单调递增，则实数a的取值范围是（ ）