题目内容
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
![]() ,
,
(1)求![]()
![]()
![]() 的值,并求出
的值,并求出![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(2)设![]() 求数列
求数列![]() 的前n项和
的前n项和![]()
(3)设![]()
![]() 在数列
在数列![]() 中取出
中取出![]() (
(![]() 为常数)项,按照原来的顺序排成一列,构成等比数列
为常数)项,按照原来的顺序排成一列,构成等比数列![]() .若对任意的数列
.若对任意的数列![]() ,均有
,均有![]() 试求
试求![]() 的最小值.
的最小值.
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]()
![]() ;
;![]()
![]() .(2)
.(2)![]()
 (3)最小值为
(3)最小值为![]() .
.
【解析】
(1)分别取![]() ,以及
,以及![]() 代入
代入![]() ,求出
,求出![]() ,猜想
,猜想![]() ,用数学归纳法证明即可,利用
,用数学归纳法证明即可,利用![]() ,即可求出
,即可求出![]() ;
;
(2)通过(1)裂项可知![]()
![]() ,分
,分![]() 为奇数和偶数两种情况讨论即可得出结论;
为奇数和偶数两种情况讨论即可得出结论;
(3)由(1)可知![]() ,根据条件分析子列
,根据条件分析子列![]() 的公比范围,将问题转化为求首项为1,公比为
的公比范围,将问题转化为求首项为1,公比为![]() 的等比数列的前
的等比数列的前![]() 项和.
项和.
解:(1)当![]() 时,
时,![]()
![]() ;
;
当![]() 时,
时,![]()
![]() ;
;
当![]() 时,
时,![]()
![]() ;
;
由此,猜测:![]()
![]()
下面用数学归纳法证明:
(i)当![]() 时,结论显然成立;
时,结论显然成立;
(ii)假设当![]()
![]() 时,
时,![]() ;
;
则当![]() 时,由条件,得
时,由条件,得
![]()
![]()

![]() .
.
即当![]() 时,结论也成立.
时,结论也成立.
于是,由(i),(ii)可知,对任意的![]() ,
,
均有![]() .
.
当![]() 时,
时,![]()
![]()
![]() .
.
又![]() ,
,
于是数列![]() 的通项公式为:
的通项公式为:![]()
![]() .
.
(2)因![]()
![]()
![]() .
.
当n为奇数时,
![]()
![]()
![]()
![]()
当n为偶数时,
![]()
![]()
![]()
![]()
故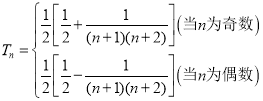

(3)因![]() ,由于数列
,由于数列![]() 的
的![]() 项子列
项子列![]() 构成等比数列,
构成等比数列,
设其公比为![]() ,则
,则
![]() .
.
因![]() ,且
,且![]()
![]()
![]() ,
,
设![]() (
(![]()
![]()
![]() ,且
,且![]() 互质)
互质)
(i)当![]() 时,因
时,因![]() ,故
,故
![]()
![]()
(ii)当![]() 时,因
时,因![]() 是数列
是数列![]() 中的项,
中的项,
故![]()
![]() .
.
从而![]()
![]()
![]()
![]()
![]()

![]()
![]()
综合(i),(ii),得:在数列![]() 中的所有
中的所有![]()
![]() 项等比子数列
项等比子数列![]() 中,
中,
其和最大的是:![]() .
.
故由题意知:![]() 的最小值为
的最小值为![]() .
.
另解(3):因![]() ,由于数列
,由于数列![]() 的
的![]()
![]() 项子列
项子列![]() 构成等比数列,
构成等比数列,
设其公比为![]() ,则
,则![]() .
.
因![]() ,且
,且![]()
![]()
![]() .
.
(i)当![]() 时,因
时,因![]() ,故
,故
![]()
![]() .
.
(ii)当![]() 时,因
时,因 ,故
,故
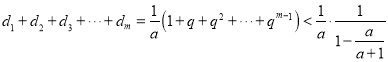
![]()
![]()
综合(i),(ii),得:在数列![]() 中的所有
中的所有![]()
![]() 项等比子数列
项等比子数列![]() 中,
中,
其和最大的是:![]() ,故由题意知:
,故由题意知:![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目