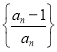
题目内容
【题目】已知数列{an}的各项均为整数,其前n项和为Sn.规定:若数列{an}满足前r项依次成公差为1的等差数列,从第r﹣1项起往后依次成公比为2的等比数列,则称数列{an}为“r关联数列”.
(1)若数列{an}为“6关联数列”,求数列{an}的通项公式;
(2)在(1)的条件下,求出Sn,并证明:对任意n∈N*,anSn≥a6S6;
(3)已知数列{an}为“r关联数列”,且a1=﹣10,是否存在正整数k,m(m>k),使得a1+a2+…+ak﹣1+ak=a1+a2+…+am﹣1+am?若存在,求出所有的k,m值;若不存在,请说明理由.
【答案】(1)![]() (或
(或![]() )
)
(2)见解析;(3)存在![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
试题(1)若数列{an}为“6关联数列”,{an}前6项为等差数列,从第5项起为等比数列,可得a6=a1+5,a5=a1+4,且![]() ,即
,即![]() ,解得a1,即可求数列{an}的通项公式;
,解得a1,即可求数列{an}的通项公式;
(2)由(1)得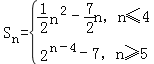 (或
(或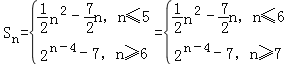 ,可见数列{anSn}的最小项为a6S6=﹣6,即可证明:对任意n∈N*,anSn≥a6S6;
,可见数列{anSn}的最小项为a6S6=﹣6,即可证明:对任意n∈N*,anSn≥a6S6;
(3)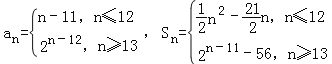 ,分类讨论,求出所有的k,m值.
,分类讨论,求出所有的k,m值.
解:(1)∵数列{an}为“6关联数列”,
∴{an}前6项为等差数列,从第5项起为等比数列,
∴a6=a1+5,a5=a1+4,且![]() ,即
,即![]() ,解得a1=﹣3
,解得a1=﹣3
∴![]() (或
(或![]() )
)
(2)由(1)得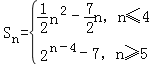 (或
(或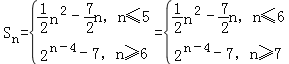 )
)
![]() ,
,
{Sn}:﹣3,﹣5,﹣6,﹣6,﹣5,﹣3,1,9,25,…{anSn}:9,10,6,0,﹣5,﹣6,4,72,400,…,
可见数列{anSn}的最小项为a6S6=﹣6,
证明: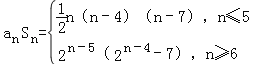 ,
,
列举法知当n≤5时,(anSn)min=a5S5=﹣5;
当n≥6时,![]() ,设t=2n﹣5,则
,设t=2n﹣5,则![]() .
.
(3)数列{an}为“r关联数列”,且a1=﹣10,∵![]()
∴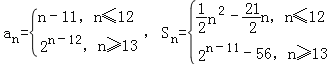
①当k<m≤12时,由![]() 得(k+m)(k﹣m)=21(k﹣m)k+m=21,k,m≤12,m>k,∴
得(k+m)(k﹣m)=21(k﹣m)k+m=21,k,m≤12,m>k,∴![]() 或
或![]() .
.
②当m>k>12时,由2k﹣11﹣56=2m﹣11﹣56得m=k,不存在
③当k≤12,m>12时,由![]() ,2m﹣10=k2﹣21k+112
,2m﹣10=k2﹣21k+112
当k=1时,2m﹣10=92,mN*;当k=2时,2m﹣10=74,mN*;
当k=3时,2m﹣10=58,mN*;当k=4时,2m﹣10=44,mN*;
当k=5时,2m﹣10=25,m=15∈N*;当k=6时,2m﹣10=22,mN*;
当k=7时,2m﹣10=14,mN*;当k=8时,2m﹣10=23,m=13∈N*;
当k=9时,2m﹣10=22,m=12舍去;当k=10时,2m﹣10=2,m=11舍去
当k=11时,2m﹣10=2,m=11舍去;当k=12时,2m﹣10=22,m=12舍去
综上所述,∴存在![]() 或
或![]() 或
或![]() 或
或![]() .
.