题目内容
如图,在棱长为1的正方体ABCD-A1B1C1D1中:(1)求异面直线BC1与AA1所成的角的大小;
(2)求三棱锥B1-A1C1B的体积;
(3)求证:B1D⊥平面A1C1B.
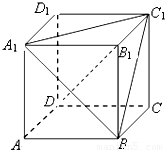
【答案】分析:(1)异面直线BC1与AA1所成的角的大小即∠B1BC1(或其补角),再由正方体的性质可得△B1BC1为等腰直角三角形,可得∠B1BC1 的大小.
(2)三棱锥B1-A1C1B的体积 即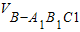 =
= •
•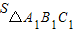 •BB1,运算求得结果.
•BB1,运算求得结果.
(3)由正方体的性质可得,由三垂线定理可得B1D⊥A1C1,同理可证,B1D⊥A1B,再根据直线和平面垂直的判定定理可得B1D⊥平面A1C1B.
解答:解:(1)由于A1A和B1B平行且相等,故异面直线BC1与AA1所成的角的大小即为BB1与BC1城的角,
故∠B1BC1(或其补角)为所求.
再由正方体的性质可得△B1BC1为等腰直角三角形,故∠B1BC1=45°,
即异面直线BC1与AA1所成的角的大小为45°.
(2)三棱锥B1-A1C1B的体积即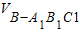 =
= •
•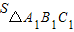 •BB1=
•BB1= ×(
×(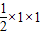 )×1=
)×1= .
.
(3)证明:由正方体的性质可得,B1D在上底面A1B1C1D1内的射影为B1D1,且A1C1⊥B1D1.
由三垂线定理可得B1D⊥A1C1.
同理可证,B1D⊥A1B.
而A1C1和 A1B是平面A1C1B内的两条相交直线,根据直线和平面垂直的判定定理,可得B1D⊥平面A1C1B.
点评:本题主要考查求异面直线所成的角,用等体积法求棱锥的体积,直线和平面垂直的判定定理的应用,属于中档题.
(2)三棱锥B1-A1C1B的体积 即
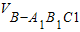 =
= •
•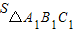 •BB1,运算求得结果.
•BB1,运算求得结果.(3)由正方体的性质可得,由三垂线定理可得B1D⊥A1C1,同理可证,B1D⊥A1B,再根据直线和平面垂直的判定定理可得B1D⊥平面A1C1B.
解答:解:(1)由于A1A和B1B平行且相等,故异面直线BC1与AA1所成的角的大小即为BB1与BC1城的角,
故∠B1BC1(或其补角)为所求.
再由正方体的性质可得△B1BC1为等腰直角三角形,故∠B1BC1=45°,
即异面直线BC1与AA1所成的角的大小为45°.
(2)三棱锥B1-A1C1B的体积即
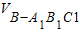 =
= •
•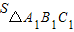 •BB1=
•BB1= ×(
×(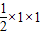 )×1=
)×1= .
.(3)证明:由正方体的性质可得,B1D在上底面A1B1C1D1内的射影为B1D1,且A1C1⊥B1D1.
由三垂线定理可得B1D⊥A1C1.
同理可证,B1D⊥A1B.
而A1C1和 A1B是平面A1C1B内的两条相交直线,根据直线和平面垂直的判定定理,可得B1D⊥平面A1C1B.
点评:本题主要考查求异面直线所成的角,用等体积法求棱锥的体积,直线和平面垂直的判定定理的应用,属于中档题.

练习册系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
