题目内容
直线y=ax与曲线(x-1)(y-1)=2(x<0)有公共点,a的取值范围是
- A.

- B.
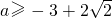
- C.

- D.以上都不对
C
分析:直线y=ax中的a看成是直线的斜率,分别画出直线与曲线的图,
由图可知,解决问题的关键是求出直线与曲线相交时,a 的范围即可.
将直线y=ax与曲线(x-1)(y-1)=2(x<0)的方程组成方程即可解得.
解答:分别画出直线与曲线的图
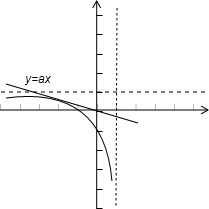
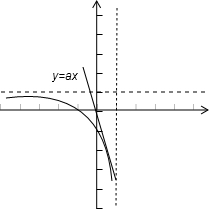
由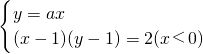
得,(x-1)(ax-1)=2(x<0),令其判断式△≥0,得 .
.
故选C.
点评:利用函数的图象可以加强直观性,同时也便于问题的理解.本题先由已知条件中的解析式,画出图形,
再利用数形结合的方法判断有公共点,a的取值范围.
分析:直线y=ax中的a看成是直线的斜率,分别画出直线与曲线的图,
由图可知,解决问题的关键是求出直线与曲线相交时,a 的范围即可.
将直线y=ax与曲线(x-1)(y-1)=2(x<0)的方程组成方程即可解得.
解答:分别画出直线与曲线的图


由
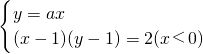
得,(x-1)(ax-1)=2(x<0),令其判断式△≥0,得
 .
.故选C.
点评:利用函数的图象可以加强直观性,同时也便于问题的理解.本题先由已知条件中的解析式,画出图形,
再利用数形结合的方法判断有公共点,a的取值范围.

练习册系列答案
相关题目
直线y=ax与曲线(x-1)(y-1)=2(x<0)有公共点,a的取值范围是( )
A、-3+2
| ||||
B、a≥-3+2
| ||||
C、-3-2
| ||||
| D、以上都不对 |