题目内容
定义域为R的偶函数f(x)满足对?x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时f(x)=-2(x-3)2,若函数y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,则a的取值范围为
- A.

- B.
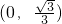
- C.

- D.

B
分析:由f(x+2)=f(x)-f(1)恒成立可知f(x)图象以x=2为对称轴,周期T=2,作出f(x)的图象,使得y=loga(x+1)的图象与f(x)的图象至少有三个交点.
解答:由f(x+2)=f(x)-f(1)得f(x+2)+f(1)=f(x),以-x代x,得f(-x+2)+f(1)=f(-x),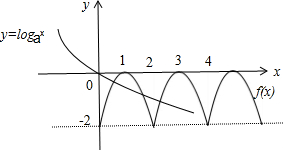
由于f(x)为偶函数,所以f(x)=f(-x),得出f(x+2)=f(-x+2)①,可知f(x)图象以x=2为对称轴.
在f(x+2)=f(x)-f(1),令x=-1,得出f(1)=f(-1)-f(1)=0,所以f(x+2)=f(x)周期T=2,
作出f(x)的图象,
∵y=loga(x+1)的图象与f(x)的图象至少有三个交点,即有loga(2+1)>f(2)=-2且0<a<1,解得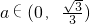 ,
,
故选B.
点评:本题考查利用函数的图象、性质的应用,函数的零点的判断.其中推导出周期性和对称性是关键.
分析:由f(x+2)=f(x)-f(1)恒成立可知f(x)图象以x=2为对称轴,周期T=2,作出f(x)的图象,使得y=loga(x+1)的图象与f(x)的图象至少有三个交点.
解答:由f(x+2)=f(x)-f(1)得f(x+2)+f(1)=f(x),以-x代x,得f(-x+2)+f(1)=f(-x),

由于f(x)为偶函数,所以f(x)=f(-x),得出f(x+2)=f(-x+2)①,可知f(x)图象以x=2为对称轴.
在f(x+2)=f(x)-f(1),令x=-1,得出f(1)=f(-1)-f(1)=0,所以f(x+2)=f(x)周期T=2,
作出f(x)的图象,
∵y=loga(x+1)的图象与f(x)的图象至少有三个交点,即有loga(2+1)>f(2)=-2且0<a<1,解得
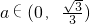 ,
,故选B.
点评:本题考查利用函数的图象、性质的应用,函数的零点的判断.其中推导出周期性和对称性是关键.

练习册系列答案
相关题目
已知定义域为R的偶函数f(x)在[0,+∞)上是增函数,且f(
)=0,则不等式f(log4x)>0的解集是
( )
| 1 |
| 2 |
( )
| A、x|x>2 | ||
B、{x|0<x<
| ||
C、{x|0<x<
| ||
D、{x|
|