题目内容
【题目】(2015·新课标I卷)如图,四边形ABCD为菱形,∠ABC=120°,E , F是平面ABCD同一侧的两点,BE⊥平面ABCD , DF⊥平面ABCD , BE=2DF , AE⊥EC.
(1)证明:平面AEC⊥平面AFC
(2)求直线AE与直线CF所成角的余弦值
【答案】
(1)
见解析
(2)
![]()
【解析】(Ⅰ)连接BD , 设BD∩AC=G , 连接EG , FG , EF , 在菱形ABCD中,不妨设GB=1,由∠ABC=120°,可得AG=GC=![]()
由BE⊥平面ABCD , AB=BC可知,AE=EC ,
又∵AE⊥EC , ∴EG=![]() ,EG⊥AC ,
,EG⊥AC ,
在Rt△EBG中,可得BE=![]() ,故DF=
,故DF=![]() .
.
在Rt△FDG中,可得FG=![]() .
.
在直角梯形BDFE中,由BD=2,BE=![]() ,DF=
,DF=![]() 可得EF=
可得EF=![]() ,∴EG2+EG2=EF2 , ∴EG⊥FG ,
,∴EG2+EG2=EF2 , ∴EG⊥FG ,
∵AC∩FG=G , ∴EG⊥平面AFC ,
∵EG![]() 面AEC , ∴平面AFC⊥平面AEC.
面AEC , ∴平面AFC⊥平面AEC. 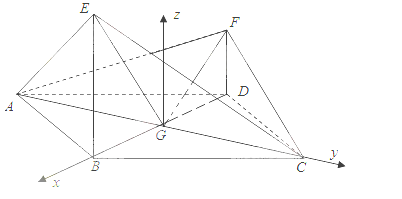
(Ⅱ)如图,以G为坐标原点,分别以![]() 的方向为x轴,y轴正方向,
的方向为x轴,y轴正方向,![]() 为单位拟长度,建立空间直角坐标系G-xyz。由(Ⅰ)可得
为单位拟长度,建立空间直角坐标系G-xyz。由(Ⅰ)可得
A(0,-![]() ),E(1,0,
),E(1,0,![]() ),F(-1,0,
),F(-1,0,![]() ),C(0,
),C(0,![]() ,0), ∴
,0), ∴![]() =(1,
=(1,![]() ,
,![]() ),
), ![]() =(-1,-
=(-1,-![]() ,
,![]() ).
).
故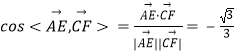 , 所以直线AE与CF所成的角的余弦值为
, 所以直线AE与CF所成的角的余弦值为![]() 。
。

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数![]() 在某一周期内的图像时,列表并填入的部分数据如下表:
在某一周期内的图像时,列表并填入的部分数据如下表:
|
|
|
|
|
|
| 0 |
|
|
|
|
| 0 | 1 | 0 |
| 0 |
| 0 |
| 0 |
| 0 |
(1)请写出上表的![]() 及函数
及函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再将所得图像上各点的横坐标缩小为原来的
个单位,再将所得图像上各点的横坐标缩小为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图像,求
的图像,求![]() 的解析式及
的解析式及 的单调递增区间;
的单调递增区间;
(3)在(2)的条件下,若![]() 在
在![]() 上恰有奇数个零点,求实数
上恰有奇数个零点,求实数![]() 与零点个数
与零点个数![]() 的值.
的值.
