题目内容
(满分12分)已知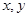 满足直线
满足直线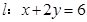 。
。
(1)求原点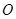 关于直线
关于直线 的对称点
的对称点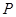 的坐标;
的坐标;
(2)当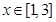 时,求
时,求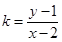 的取值范围。
的取值范围。
【答案】
(1)  ;(2)
;(2)  。
。
【解析】本试题主要是考查了直线的方程以及点关于直线对称点的坐标的求解
和斜率几何意义的灵活运用。
(1)设对称后的点P(x,y),那么满足OP的中点在直线上,和OP的斜率与已知直线的斜率互为负倒数得到结论。
(2)根据斜率公式可知,表示的为动点(x,y)到定点(2,1)的两点的斜率的取值范围。
解(1)求得点 ;
;
(2) ,求得
,求得 ,从而
,从而

 。
。

练习册系列答案
相关题目
(本小题满分12分)如图所示,已知圆![]()
|
足![]() 的轨迹为曲线E.
的轨迹为曲线E.
(1)求曲线E的方程;(II)若过定点F(0,2)
的直线交曲线E于不同的两点G、H(点G在点F、H之间),
且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
(本题满分12分)某校高三年级文科学生600名,从参加期末考试的学生中随机抽出某班学生(该班共50名同学),并统计了他们的数学成绩(成绩均为整数且满分为150分),数学成绩分组及各组频数如下表: (Ⅰ)写出a、b的值;
(Ⅱ)估计该校文科生数学成绩在120分以上学生人数;
(Ⅲ)该班为提高整体数学成绩,决定成立“二帮一”小组,即从成绩在[135,150]中选两位同学,来帮助成绩在[45,60)中的某一位同学.已知甲同学的成绩为56分, 乙同学的成绩为145分,求甲乙在同一小组的概率.
| 分组 | 频数 | 频率 |
| [45,60) | 2 | 0.04 |
| [60,75) | 4 | 0.08 |
| [75,90) | 8 | 0.16 |
| [90,105) | 11 | 0.22 |
| [105,120) | 15 | 0.30 |
| [120,135) | a | b |
| [135,150] | 4 | 0.08 |
| 合计 | 50 | 1 |
 .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为 ,且过点
,且过点 .
. 的达式;
的达式; ,
, ,角C为锐角。且满
,角C为锐角。且满 ,求c的值.
,求c的值.