题目内容
如图,在△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,沿AD把△ABC折起,使∠BCD=90°。
(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设E为BC的中点,求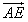 与
与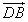 夹角的余弦值。
夹角的余弦值。
(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设E为BC的中点,求
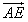 与
与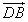 夹角的余弦值。
夹角的余弦值。 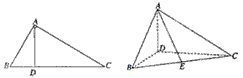
| (Ⅰ)证明:∵折起前AD是BC边上的高, ∴当ΔABD折起后,AD⊥DC,AD⊥DB, 又DB∩DC=D, ∴AD⊥平面BDC, ∵AD  平面ADB, 平面ADB, ∴平面ADB⊥平面BDC。 |
|
| (Ⅱ )解:由∠BDC=90°及(Ⅰ)知DA,DB,DC两两垂直, 不妨设|DB|=1, 以D为坐标原点,以所在直线x,y,z轴建立如图所示的空间直角坐标系, 易得D(0,0,0),B(1,0,0),C(0,3,0), A(0,0,  ),E( ),E( , , ,0), ,0),∴  , , =(1,0,0), =(1,0,0),∴  与 与 夹角的余弦值为 夹角的余弦值为 。 。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知