题目内容
如图，△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面BCD，AB⊥平面BCD，AB=2| 3 |
（Ⅰ）求证：CD⊥平面ABM；
（Ⅱ）求直线AM与平面BCD所成角的大小．
分析：（I）取CD中点O，连OB，OM，根据面面垂直的性质定理及等腰三角形三线合一的性质可得OM⊥平面BCD，进而根据线面垂直的性质定理可得OM∥AB，即O，M，A，B四点共面，最后由线面垂直的判定定理得到CD⊥平面ABM；
（Ⅱ）延长AM、BO相交于E，根据线面所成角的定义可知∠AEB就是AM与平面BCD所成的角，在三角形AEB中求出此角即可；
（Ⅱ）延长AM、BO相交于E，根据线面所成角的定义可知∠AEB就是AM与平面BCD所成的角，在三角形AEB中求出此角即可；
解答：解：（I）取CD中点O，连OB，OM，则OB⊥CD，OM⊥CD．
∵平面MCD⊥平面BCD，平面MCD∩平面BCD=CD，OM?平面MCD
∴OM⊥平面BCD，
又∵AB⊥平面BCD，
∴OM∥AB，即O，M，A，B四点共面
∴OB，OM?平面ABM，
又∵OB∩OM=O
故CD⊥平面ABM；
（II）延长AM、BO相交于E，
∵AB⊥平面BCD，
则∠AEB就是AM与平面BCD所成的角．
OB=MO=
，MO∥AB，则
=
=
，EOEO=OB=
，
所以EB=2
=AB，
故∠AEB=45°
即直线AM与平面BCD所成角的大小为45°．
∵平面MCD⊥平面BCD，平面MCD∩平面BCD=CD，OM?平面MCD
∴OM⊥平面BCD，
又∵AB⊥平面BCD，
∴OM∥AB，即O，M，A，B四点共面
∴OB，OM?平面ABM，
又∵OB∩OM=O
故CD⊥平面ABM；
（II）延长AM、BO相交于E，
∵AB⊥平面BCD，
则∠AEB就是AM与平面BCD所成的角．
OB=MO=
| 3 |
| EO |
| EB |
| MO |
| AB |
| 1 |
| 2 |
| 3 |
所以EB=2
| 3 |
故∠AEB=45°
即直线AM与平面BCD所成角的大小为45°．
点评：本题考查的知识点是直线与平面所成的角，直线与平面垂直的判定，解答（I）的关键是熟练掌握空间线线关系，线面有关系及面面关系之间的相互转化，解答（II）的关键是构造出线面夹角的平面角．
练习册系列答案
阅读快车系列答案
相关题目
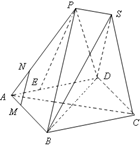已知四边形ABCD为菱形，AB=6，∠BAD=60°，两个正三棱锥P-ABD、S-BCD（底面是正三角形且顶点在底面上的射影是底面正三角形的中心）的侧棱长都相等，如图，E、M、N分别在AD、
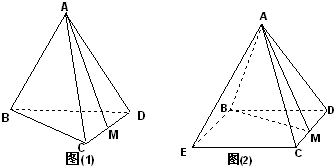正四面体A-BCD的棱长为1，（Ⅰ）如图（1）M为CD中点，求异面直线AM与BC所成的角；（Ⅱ）将正四面体沿AB、BD、DC、BC剪开，作为正四棱锥的侧面如图（2），求二面角M-AB-E的大小；（Ⅲ）若将图（1）与图（2）面ACD重合，问该几何体是几面体（不需要证明），并求这几何体的体积．
正四面体A-BCD的棱长为1，（Ⅰ）如图（1）M为CD中点，求异面直线AM与BC所成的角；（Ⅱ）将正四面体沿AB、BD、DC、BC剪开，作为正四棱锥的侧面如图（2），求二面角M-AB-E的大小；（Ⅲ）若将图（1）与图（2）面ACD重合，问该几何体是几面体（不需要证明），并求这几何体的体积．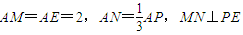
．
．