题目内容
14.已知映射f:P(m,n)→P′(-m,2n)(m≥0,n≥0).设点A(1,3),B(3,1),点M是线段AB上一动点,f:M→M′.当点M是线段AB的中点时,点M′的坐标是(-2,4);当点M在线段AB上从点A开始运动到点B结束时,点M的对应点M'所经过的路线长度为$2\sqrt{5}$.分析 根据所给的两个点的坐标写出直线的方程,设出两个点的坐标,根据所给的映射的对应法则得到两个点坐标之间的关系,代入直线的方程即可得到结论.
解答 解:线段AB的中点M(2,2),则M′(-2,4),
∵A(1,3),B(3,1),
∴AB的方程为$\frac{y-1}{3-1}=\frac{x-3}{1-3}$,即x+y=4,
设P(x1,y1),P′(-x1,2y1),且x1+y1=4
设$\left\{\begin{array}{l}{x=-{x}_{1}}\\{y=2{y}_{1}}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}_{1}=-x}\\{{y}_{1}=\frac{y}{2}}\end{array}\right.$,
则-x+$\frac{y}{2}$=4,
即y=2x+8,
则M′对应的轨迹为直线y=2x+8,
A′(-1,6),B′(-3,2),
则|A′B′|=$\sqrt{(-1+3)^{2}+(6-2)^{2}}$=$\sqrt{4+16}=\sqrt{20}$=$2\sqrt{5}$,
故答案为:(-2,4),$2\sqrt{5}$.
点评 本题主要考查映射的应用,以及两点间的距离公式的应用,考查学生的转化能力.

练习册系列答案
相关题目
9.已知向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(4,x),$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数x的值是( )
| A. | 0 | B. | ±2 | C. | 2 | D. | -2 |

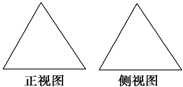 如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )
如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )