题目内容
定义运算a*b=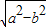 ,a⊕b=
,a⊕b=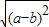 ,则函数f(x)=
,则函数f(x)=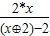 的奇偶性为 .
的奇偶性为 .
【答案】分析:先根据运算表示出函数f(x)的解析式,再求出其定义域,然后在满足定义域的前提下化简函数f(x),最后根据函数奇偶性的定义可求出函数f(x)为奇函数.
解答:解:∵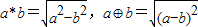
∴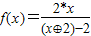 =
=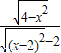
∴4-x2≥0,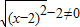
∴-2≤x≤2,且x≠0
函数f(x)的定义域为:{x|-2≤x≤2,且x≠0}
∴f(x)=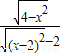 =
=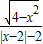 =
=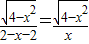
f(-x)=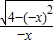 =
=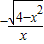 =-f(x)
=-f(x)
故函数f(x)为奇函数.
故答案为:奇函数.
点评:本题主要考查求函数的基本性质--定义域、奇偶性.考查考生接受和运用新知识的能力.
解答:解:∵
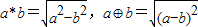
∴
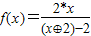 =
=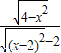
∴4-x2≥0,
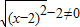
∴-2≤x≤2,且x≠0
函数f(x)的定义域为:{x|-2≤x≤2,且x≠0}
∴f(x)=
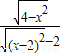 =
=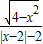 =
=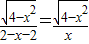
f(-x)=
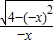 =
=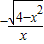 =-f(x)
=-f(x)故函数f(x)为奇函数.
故答案为:奇函数.
点评:本题主要考查求函数的基本性质--定义域、奇偶性.考查考生接受和运用新知识的能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目