题目内容
a和b是两条异面直线,下列结论正确的个数是( )
(1) 过不在a、b上的任一点,可作一个平面与a、b都平行.
(2) 过不在a、b上的任一点,可作一条直线与a、b都相交.
(3) 过a可以并且只可以作一个平面与b平行.
(4) 过不在a、b上的任一点,可作一条直线与a、b都垂直.
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:(1)过点作平面和直线 平行的平面可能正好经过直线
平行的平面可能正好经过直线 ,(1)错;(2)过点和直线
,(1)错;(2)过点和直线 确定的平面和
确定的平面和 平行时,满足条件的直线不存在,(2)错;(3)在
平行时,满足条件的直线不存在,(2)错;(3)在 上任取一点
上任取一点 ,过点
,过点 作
作 ∥
∥ ,过
,过 ,
, 可确定面
可确定面 ,则
,则 ∥
∥ ,(3)正确;(4)作面
,(3)正确;(4)作面 ,使得
,使得 ∥
∥ ,
, ∥
∥ ,只需作
,只需作 ,则
,则 ,(4)正确.
,(4)正确.
考点:1、线面平行的判定;2、线和线的位置关系;

练习册系列答案
相关题目
下列命题中正确的个数是( ).
(1)若直线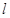 上有无数个点不在平面
上有无数个点不在平面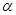 内,则
内,则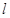 ∥
∥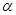 .
.
(2)若直线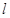 与平面
与平面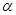 平行,则
平行,则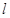 与平面
与平面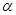 内的任意一条直线都平行.
内的任意一条直线都平行.
(3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.
(4)若直线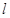 与平面
与平面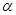 平行,则
平行,则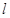 与平面
与平面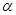 内的任意一条直线都没有公共点.
内的任意一条直线都没有公共点.
| A.0 | B.1 | C.2 | D.3 |
下列四个命题中错误的是( )
A.若直线 、 、 互相平行,则直线 互相平行,则直线 、 、 确定一个平面 确定一个平面 |
| B.若四点不共面,则这四点中任意三点都不共线 |
| C.若两条直线没有公共点,则这两条直线是异面直线 |
| D.两条异面直线不可能垂直于同一个平面 |
在下列条件下,可判断平面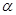 与平面
与平面 平行的是( )
平行的是( )
| A.α、β都垂直于平面γ |
| B.α内不共线的三个点到β的距离相等 |
| C.l,m是α内两条直线且l∥β,m∥β |
| D.l,m是异面直线,且l∥α,m∥α,l∥β,m∥β |
设 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
下列命题正确的是( )
| A.若两条直线和同一个平面所成的角相等, 则这两条直线平行; |
| B.若一个平面内有三点到另一个平面的距离相等,则这两个平面平行; |
| C.若一条直线和两个相交平面都平行, 则这条直线与这两个平面的交线平行; |
| D.若两个平面都垂直于第三个平面, 则这两个平面平行. |
设 是三条不同的直线,
是三条不同的直线, 是三个不同的平面,则下列命题不正确的是( )
是三个不同的平面,则下列命题不正确的是( )
A.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
B.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
C.若 ∥ ∥ , ,   ,则 ,则 ∥ ∥ |
D.若 ∥ ∥ , , ∥ ∥ ,则 ,则 不一定平行于 不一定平行于 |