题目内容
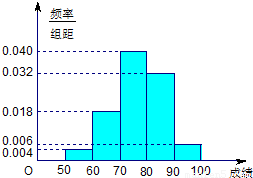 某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].下图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].下图是按上述分组方法得到的频率分布直方图.(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在[50,60)∪[90,100]内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“|m-n|>10”概率.
【答案】分析:(1)先算出频率分布直方图成绩大于或等于60且小于80的频率,再利用频数等于频率×样本总数即可解得全班学生中成绩合格的人数.
(2)欲求事件“|m-n|>10”概率,根据古典概型,算出基本事件的总个数n和算出事件事件“|m-n|>10”中包含的基本事件的个数m;最后 算出事件A的概率,即P(A)=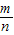 .
.
解答:解:(I)由直方图知,成绩在[60,80)内的人数为:50×10×(0.18+0.040)=29.
所以该班在这次数学测试中成绩合格的有29人.(3分)
(II)由直方图知,成绩在[50,60)内的人数为:50×10×0.004=2,
设成绩为x、y(5分)
成绩在[90,100]的人数为50×10×0.006=3,设成绩为a、b、c,(6分)
若m,n∈[50,60)时,只有xy一种情况,(7分)
若m,n∈[90,100]时,有ab,bc,ac三种情况,(8分)
若m,n分别在[50,60)和[90,100]内时,有
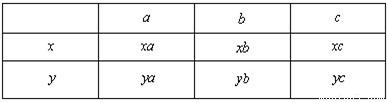
共有6种情况,所以基本事件总数为10种,(9分)
事件“|m-n|>10”所包含的基本事件个数有6种(10分)
∴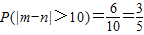 .(12分)
.(12分)
点评:在频率分布直方图中,每一个小矩形都是等宽的,即等于组距,高是 ,所以有:
,所以有: ×组距=频率;即可把所求范围内的频率求出,进而求该范围的人数.
×组距=频率;即可把所求范围内的频率求出,进而求该范围的人数.
(2)欲求事件“|m-n|>10”概率,根据古典概型,算出基本事件的总个数n和算出事件事件“|m-n|>10”中包含的基本事件的个数m;最后 算出事件A的概率,即P(A)=
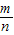 .
.解答:解:(I)由直方图知,成绩在[60,80)内的人数为:50×10×(0.18+0.040)=29.
所以该班在这次数学测试中成绩合格的有29人.(3分)
(II)由直方图知,成绩在[50,60)内的人数为:50×10×0.004=2,
设成绩为x、y(5分)
成绩在[90,100]的人数为50×10×0.006=3,设成绩为a、b、c,(6分)
若m,n∈[50,60)时,只有xy一种情况,(7分)
若m,n∈[90,100]时,有ab,bc,ac三种情况,(8分)
若m,n分别在[50,60)和[90,100]内时,有

共有6种情况,所以基本事件总数为10种,(9分)
事件“|m-n|>10”所包含的基本事件个数有6种(10分)
∴
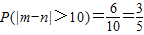 .(12分)
.(12分)点评:在频率分布直方图中,每一个小矩形都是等宽的,即等于组距,高是
 ,所以有:
,所以有: ×组距=频率;即可把所求范围内的频率求出,进而求该范围的人数.
×组距=频率;即可把所求范围内的频率求出,进而求该范围的人数. 
练习册系列答案
相关题目
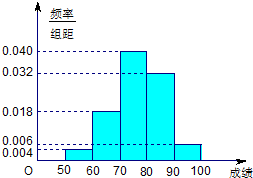 某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.
某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.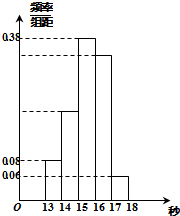 某班50名学生在一次百米测试中,成绩全部在[13,18]内,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15);…第五组[17,18].右图是按上述分组方法得到的频率分布直方图.且第一组,第二组,第四组的频数成等比数列,m,n表示该班某两位同学的百米测试成绩,且m,n∈[13,14)∪[17,18].则事件“|m-n|>1”的概率为( )
某班50名学生在一次百米测试中,成绩全部在[13,18]内,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15);…第五组[17,18].右图是按上述分组方法得到的频率分布直方图.且第一组,第二组,第四组的频数成等比数列,m,n表示该班某两位同学的百米测试成绩,且m,n∈[13,14)∪[17,18].则事件“|m-n|>1”的概率为( )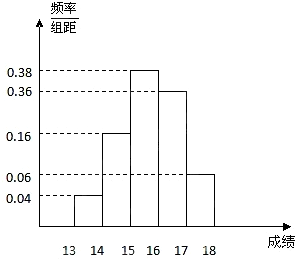 某班50名学生在一次百米测试中,成绩介于13秒与18秒之间.将测试结果分成五组,按上述分组方法得到如下频率分布直方图
某班50名学生在一次百米测试中,成绩介于13秒与18秒之间.将测试结果分成五组,按上述分组方法得到如下频率分布直方图
 某班 50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )
某班 50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )