题目内容
11.边长为2的两个等边△ABD,△CBD所在的平面互相垂直,则四面体ABCD的体积是1.分析 取DB中点O,连结AO,CO,易得AO⊥面BCD,再利用体积公式即可求解.
解答  解:如图,取DB中点O,连结AO,CO,
解:如图,取DB中点O,连结AO,CO,
∵△ABD,△CBD边长为2的两个等边△‘
∴AO⊥BD,CO⊥BD,又∵面ABD⊥面BDC;
∴AO⊥面BCD,AO=$\sqrt{3}$,
四面体ABCD的体积v=$\frac{1}{3}×{s}_{△BCD}×AO=\frac{1}{3}×\sqrt{3}×\sqrt{3}=1$,
故答案为:1.
点评 本题考查了三棱锥的体积的求解,关键是找出面的垂线,属于基础题.

练习册系列答案
相关题目
1.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F做圆x2+y2=a2的切线,切点为M,切线交y轴于点P,且$\overrightarrow{FM}$=2$\overrightarrow{MP}$,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
2.某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻两个月的概率;
(2)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程y=bx+a;
(附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$)
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
(1)求选取的2组数据恰好是相邻两个月的概率;
(2)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程y=bx+a;
(附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$)
20.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(-$\frac{π}{6}$)的值为( )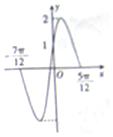

| A. | -1 | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
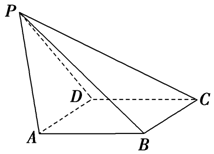 如图,已知四棱锥P-ABCD,侧面PAD是正三角形,底面ABCD是菱形,∠BAD=60°,设平面PAD∩平面PBC=l.
如图,已知四棱锥P-ABCD,侧面PAD是正三角形,底面ABCD是菱形,∠BAD=60°,设平面PAD∩平面PBC=l.