题目内容

某次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题，并宣
布：观众答对问题A可获奖金2a元；答对问题B可获奖金3a元，答对两题则可获5a元.先答哪个问题由观众选择，只有第1题答对才能答第2题，否则中止答题.若你被选为幸运观众，且假设你答对A、B的概率分别为、，你觉得应先回答哪个问题？说明理由.
先回答问题A.
解：若先回答问题A,设获得奖金为X，X的分布列如下：
X
0
2a
5a
P



 
所以EX=0×+2a×+5a×=
若先回答问题A,设获得奖金为Y，Y的分布列如下：
Y
0
3a
5a
P



 
所以EY=0×+3a×+5a×=，从而EX>EY,所以应先回答问题A.
练习册系列答案
相关题目
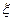湖南省有许多旅游景点，某同学利用寒暑假旅游了张家界、南岳、韶山、岳阳楼和桃花源等5个景点，并收藏有张家界纪念门票3张，南岳纪念门票2张，韶山、岳阳楼、桃花源纪念门票各1张，现从中随机抽取5张.
（Ⅰ）求抽取的5张门票中恰有3个或恰有4个景点的概率；
（Ⅱ）若抽取的5张门票中5个景点都有记10分，恰有4个景点记8分，恰有3个景点记6分，依此类推.设表示所得的分数，求的分布列和数学期望.
在某校组织的一次篮球定点投篮训练中，规定每人最多投次；在处每投进一球得分，在处每投进一球得分；如果前两次得分之和超过分即停止投篮，否则投第三次.同学在处的命中率为0，在处的命中率为，该同学选择先在处投一球，以后都在处投，用表示该同学投篮训练结束后所得的总分，其分布列为
          
        
             
     
     
      
           
          
                
           
         
             
  （1）求的值；
（2）求随机变量的数学期望；                        
（3）试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
某运动员投篮中的概率P＝0.6
（1）求一次投篮时投中次数ξ的期望和方差;
（2）求重复5次投篮时投中次数η的期望与方差.
设ξ~B（n，p）且Eξ=15，Dξ=，则n、p的值分别是
A．50，B．60，C．50，D．60，
已知离散型随机变量的概率分布如下：

1
3
5
P
0.5
m
0.2
则其数学期望E等于（   ）.
A．1B．0.6C．D．2.4
一个袋子里装有大小相同的3个红球和2个黄球，从中取出2个，含红球个数的数学期望是            .
厂家在产品出厂前，需对产品做检验，厂家将一批产品发给商家时，商家按合同规定也需随机抽取一定数量的产品做检验，以决定是否接收这批产品.
（Ⅰ）若厂家库房中的每件产品合格的概率为0.8，从中任意取出4件进行检验.求至少有1件是合格品的概率;
（Ⅱ）若厂家发给商家20件产品，其中有3件不合格，按合同规定该商家从中任取2件，都进行检验，只有2件都合格时才接收这批产品，否则拒收.求该商家可能检验出不合格产品数的分布列及期望，并求该商家拒收这批产品的概率.
奖器有10个小球，其中8个小球上标有数字2，2个小球上标有数字5，现摇出3个小球，规定所得奖金（元）为这3个小球上记号之和．
（1）求奖金为9元的概率
（2）（非实验班做）求此次摇奖获得奖金数额的分布列．
（实验班做）求此次摇奖获得奖金数额的分布列，期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网