题目内容
已知函数
(1)求函数f(x)的最小正周期和图象的对称轴方程及对称中心;
(2)求函数f(x)在区间 上的值域.
上的值域.
解:
=
= cos2x+
cos2x+ sin2x+sin(2x-
sin2x+sin(2x- )
)
= cos2x+
cos2x+ sin2x-
sin2x- cos2x
cos2x
=- cos2x+
cos2x+ sin2x
sin2x
=sin(2x- ).
).
最小正周期 T= =π,
=π,
由2x- =kπ+
=kπ+ ,k∈Z得图象的对称轴方程 x=
,k∈Z得图象的对称轴方程 x=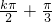 ,k∈Z
,k∈Z
由2x- =kπ,k∈Z得x=
=kπ,k∈Z得x= ,对称中心(
,对称中心( ,0),k∈Z
,0),k∈Z
(2)当x∈ 时,2x-
时,2x- ∈[
∈[ ,
, ],由正弦函数的性质得值域为[
],由正弦函数的性质得值域为[ ].
].
分析:利用两角差的余弦公式,诱导公式及二倍角正弦公式将f(x)化为一角一函数形式得出f(x)=sin(2x- ).
).
将2x- 看作整体(1)借助于正弦函数的对称轴方程及对称中心求解(2)先求出2x-
看作整体(1)借助于正弦函数的对称轴方程及对称中心求解(2)先求出2x- 的范围,再求出值域.
的范围,再求出值域.
点评:本题考查利用三角公式进行恒等变形的技能以及运算能力,三角函数的图象和性质,整体换元的思想方法.

=

=
 cos2x+
cos2x+ sin2x+sin(2x-
sin2x+sin(2x- )
)=
 cos2x+
cos2x+ sin2x-
sin2x- cos2x
cos2x=-
 cos2x+
cos2x+ sin2x
sin2x=sin(2x-
 ).
).最小正周期 T=
 =π,
=π,由2x-
 =kπ+
=kπ+ ,k∈Z得图象的对称轴方程 x=
,k∈Z得图象的对称轴方程 x=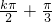 ,k∈Z
,k∈Z由2x-
 =kπ,k∈Z得x=
=kπ,k∈Z得x= ,对称中心(
,对称中心( ,0),k∈Z
,0),k∈Z(2)当x∈
 时,2x-
时,2x- ∈[
∈[ ,
, ],由正弦函数的性质得值域为[
],由正弦函数的性质得值域为[ ].
].分析:利用两角差的余弦公式,诱导公式及二倍角正弦公式将f(x)化为一角一函数形式得出f(x)=sin(2x-
 ).
).将2x-
 看作整体(1)借助于正弦函数的对称轴方程及对称中心求解(2)先求出2x-
看作整体(1)借助于正弦函数的对称轴方程及对称中心求解(2)先求出2x- 的范围,再求出值域.
的范围,再求出值域.点评:本题考查利用三角公式进行恒等变形的技能以及运算能力,三角函数的图象和性质,整体换元的思想方法.

练习册系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线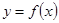 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)