题目内容
 在多面体ABCDEF中,△ADE是边长为2的等边三角形,EF∥平面ABCD,AB⊥平面ADE,AB=
在多面体ABCDEF中,△ADE是边长为2的等边三角形,EF∥平面ABCD,AB⊥平面ADE,AB= ,EF=
,EF= .
.
(1)求证AB∥DC;
(2)求直线BE与平面ABCD所成的角;
(3)若DF⊥FC,求证DF⊥BC.
解:
(1)证明:∵EF∥平面ABCD,平面ABEF∩平面ABCD=AB,
∴AB∥EF,同理 CD∥EF
AB∥CD.
(2)∵AB⊥平面ADE,
∴平面ADE⊥平面ABCD,取AD的中点O,连接 EO、BO,
△ADE是等边三角形,EO⊥AD,
∴EO⊥平面ABCD,∠EBO为直线BE与平面ABCD所成的角,在△EBO中,
tan∠EBO= =
= ,故直线BE与平面ABCD所成的角等于30°.
,故直线BE与平面ABCD所成的角等于30°.
(3)∵AB⊥平面ADE,EF∥AB,
∴EF⊥平面ADE,△ADE是边长为2的等边三角形,
BD2=AD2+AB2=4+8=12,DF2=DE2+EF2=4+2=6,
BF2=AE2+(AB-EF)2=4+2=6,∴DF⊥BF.
又 DF⊥FC,BF∩FC=F,∴DF⊥平面FBC,∴DF⊥BC.
分析:(1)由线面平行的性质得AB∥EF,同理 CD∥EF,故由AB∥CD.
(2)先证平面ADE⊥平面ABCD,取AD的中点O,,∠EBO为直线BE与平面ABCD所成的角,将此角放到直角三角形中,利用直角三角形中的边角关系求出此角的大小.
(3)利用勾股定理证明DF⊥BF,再根据 DF⊥FC,从而证明DF⊥平面FBC,故DF⊥BC.
点评:本题考查线面平行的性质,求直线和平面所成的角的大小,通过证明线面垂直达到证明线线垂直的目的.
(1)证明:∵EF∥平面ABCD,平面ABEF∩平面ABCD=AB,
∴AB∥EF,同理 CD∥EF
AB∥CD.
(2)∵AB⊥平面ADE,
∴平面ADE⊥平面ABCD,取AD的中点O,连接 EO、BO,
△ADE是等边三角形,EO⊥AD,
∴EO⊥平面ABCD,∠EBO为直线BE与平面ABCD所成的角,在△EBO中,
tan∠EBO=
 =
= ,故直线BE与平面ABCD所成的角等于30°.
,故直线BE与平面ABCD所成的角等于30°.(3)∵AB⊥平面ADE,EF∥AB,
∴EF⊥平面ADE,△ADE是边长为2的等边三角形,
BD2=AD2+AB2=4+8=12,DF2=DE2+EF2=4+2=6,
BF2=AE2+(AB-EF)2=4+2=6,∴DF⊥BF.
又 DF⊥FC,BF∩FC=F,∴DF⊥平面FBC,∴DF⊥BC.
分析:(1)由线面平行的性质得AB∥EF,同理 CD∥EF,故由AB∥CD.
(2)先证平面ADE⊥平面ABCD,取AD的中点O,,∠EBO为直线BE与平面ABCD所成的角,将此角放到直角三角形中,利用直角三角形中的边角关系求出此角的大小.
(3)利用勾股定理证明DF⊥BF,再根据 DF⊥FC,从而证明DF⊥平面FBC,故DF⊥BC.
点评:本题考查线面平行的性质,求直线和平面所成的角的大小,通过证明线面垂直达到证明线线垂直的目的.

练习册系列答案
相关题目
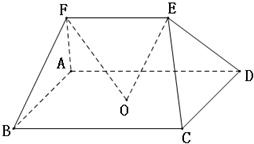 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,平面CDE是等边三角形,棱EF∥BC且EF=
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,平面CDE是等边三角形,棱EF∥BC且EF=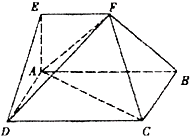 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.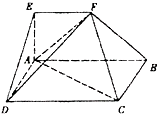 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF,∠EAB=90°,平面ABFE⊥平面ABCD.
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF,∠EAB=90°,平面ABFE⊥平面ABCD.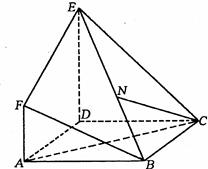 如图,在多面体ABCDEF中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2
如图,在多面体ABCDEF中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2