题目内容
已知二次函数f(x)=ax2+bx+c的图象与x轴有两个不同的交点,若f(c)=0且0<x<c时,f(x)>0,
(1)证明: 是f(x)=0的一个根;
是f(x)=0的一个根;
(2)试比较 与c的大小;
与c的大小;
(3)证明:-2<b<-1.
(1)证明:
 是f(x)=0的一个根;
是f(x)=0的一个根;(2)试比较
 与c的大小;
与c的大小;(3)证明:-2<b<-1.
(1)见解析 (2) >c. (3)见解析
>c. (3)见解析
 >c. (3)见解析
>c. (3)见解析解:(1)证明:∵f(x)的图象与x轴有两个不同的交点,
∴f(x)=0有两个不等实根x1,x2,
∵f(c)=0,
∴x1=c是f(x)=0的根,
又x1x2= ,
,
∴x2= (
( ≠c),
≠c),
∴ 是f(x)=0的一个根.
是f(x)=0的一个根.
(2)假设 <c,又
<c,又 >0,
>0,
由0<x<c时,f(x)>0,
知f( )>0与f(
)>0与f( )=0矛盾,∴
)=0矛盾,∴ ≥c,
≥c,
又∵ ≠c,∴
≠c,∴ >c.
>c.
(3)证明:由f(c)=0,得ac+b+1=0,
∴b=-1-ac.
又a>0,c>0,∴b<-1.
二次函数f(x)的图象的对称轴方程为
x=- =
= <
< =x2=
=x2= ,
,
即- <
< .
.
又a>0,∴b>-2,
∴-2<b<-1.
∴f(x)=0有两个不等实根x1,x2,
∵f(c)=0,
∴x1=c是f(x)=0的根,
又x1x2=
 ,
,∴x2=
 (
( ≠c),
≠c),∴
 是f(x)=0的一个根.
是f(x)=0的一个根.(2)假设
 <c,又
<c,又 >0,
>0,由0<x<c时,f(x)>0,
知f(
 )>0与f(
)>0与f( )=0矛盾,∴
)=0矛盾,∴ ≥c,
≥c,又∵
 ≠c,∴
≠c,∴ >c.
>c.(3)证明:由f(c)=0,得ac+b+1=0,
∴b=-1-ac.
又a>0,c>0,∴b<-1.
二次函数f(x)的图象的对称轴方程为
x=-
 =
= <
< =x2=
=x2= ,
,即-
 <
< .
.又a>0,∴b>-2,
∴-2<b<-1.

练习册系列答案
相关题目
 ,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1.
,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1. 有有理根,那么
有有理根,那么 中至少有一个是偶数时,下列假设中正确的是
中至少有一个是偶数时,下列假设中正确的是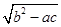 <
<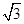 a”索的因应是( )
a”索的因应是( ) ,(2)
,(2) ,(3)
,(3) 中至少有一个方程有实根,求实数
中至少有一个方程有实根,求实数 的取值范围.
的取值范围.