题目内容
定义在区间(-1,1)内的函数f(x)满足2f(x)-f(-x)=lg(x+1),则f(x)=
lg(x+1)+
lg(1-x)
lg(x+1)+
lg(1-x).
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
分析:因为2f(x)-f(-x)=lg(x+1),用-x代替x,得,2f(-x)-f(x)=lg(-x+1),两式联立消去f(-x),就可求出
f(x).
f(x).
解答:解:∵2f(x)-f(-x)=lg(x+1),①
∴2f(-x)-f(x)=lg(-x+1),②
①×2+①,得,3f(x)=2lg(x+1)+lg(1-x)
∴f(x)=
lg(x+1)+
lg(1-x)
故答案为
lg(x+1)+
lg(1-x)
∴2f(-x)-f(x)=lg(-x+1),②
①×2+①,得,3f(x)=2lg(x+1)+lg(1-x)
∴f(x)=
| 2 |
| 3 |
| 1 |
| 3 |
故答案为
| 2 |
| 3 |
| 1 |
| 3 |
点评:本题主要考查利用方程的思想求函数解析式,关键是如何消掉2f(x)-f(-x)=lg(x+1)中的f(-x).

练习册系列答案
相关题目
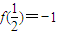 ,对任意x、y∈(-1,1),恒有
,对任意x、y∈(-1,1),恒有 成立,又数列an满足
成立,又数列an满足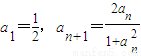 ,设
,设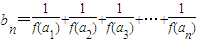 .
.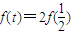 ;
;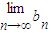 的值;
的值;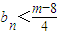 成立?若存在,求出m的最小值;若不存在,请说明理由.
成立?若存在,求出m的最小值;若不存在,请说明理由. ,对任意x、y∈(-1,1),恒有
,对任意x、y∈(-1,1),恒有 成立,又数列an满足
成立,又数列an满足 ,设
,设 .
. ;
; 的值;
的值; 成立?若存在,求出m的最小值;若不存在,请说明理由.
成立?若存在,求出m的最小值;若不存在,请说明理由.