题目内容
已知函数f(x)定义在区间(-1,1)上,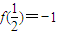 ,对任意x、y∈(-1,1),恒有
,对任意x、y∈(-1,1),恒有 成立,又数列an满足
成立,又数列an满足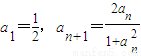 ,设
,设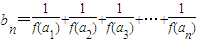 .
.(1)在(-1,1)内求一个实数t,使得
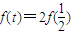 ;
;(2)证明数列f(an)是等比数列,并求f(an)的表达式和
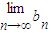 的值;
的值;(3)是否存在m∈N*,使得对任意n∈N*,都有
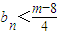 成立?若存在,求出m的最小值;若不存在,请说明理由.
成立?若存在,求出m的最小值;若不存在,请说明理由.
【答案】分析:(1)直接利用条件把2f( )进行转化代入已知即可求出实数t;
)进行转化代入已知即可求出实数t;
(2)把f(an+1)利用已知条件进行整理得到f(an+1)与f(an)之间的关系式,即可证明数列f(an)是等比数列,进而求f(an)的表达式;利用求得的f(an)的表达式代入即可求出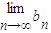 的值;
的值;
(3)利用(2)的结论求出bn的表达式,代入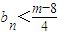 ,整理后把
,整理后把 恒成立问题转化为
恒成立问题转化为 恒成立,最后利用函数的单调性求出
恒成立,最后利用函数的单调性求出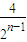 的最值即可求出m的最小值.
的最值即可求出m的最小值.
解答:解:(1)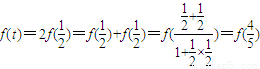 ,
,
∴ (3分)
(3分)
(2)∵ ,且
,且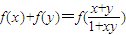
∴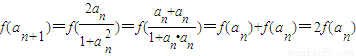 ,
,
即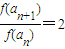
∴f(an)是以-1为首项,2为公比的等比数列,(2分)
∴f(an)=-2n-1.(4分)
∴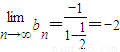 .(8分)
.(8分)
(3)由(2)得,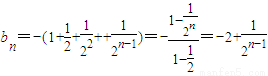 .(1分)
.(1分)
若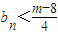 对任意n∈N*恒成立,即
对任意n∈N*恒成立,即 ,
, 恒成立(3分)
恒成立(3分)
∵n∈N*,∴当n=1时, 有最大值4,故m>4.(5分)
有最大值4,故m>4.(5分)
又m∈N*,∴存在m≥5,使得对任意n∈N*,有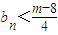 .
.
所以mmin=5.(7分)
点评:本题是对数列和函数知识的综合考查.这一类型题,一般都是利用函数的性质来研究数列的性质,做题的关键是把函数的性质理解透彻.
 )进行转化代入已知即可求出实数t;
)进行转化代入已知即可求出实数t;(2)把f(an+1)利用已知条件进行整理得到f(an+1)与f(an)之间的关系式,即可证明数列f(an)是等比数列,进而求f(an)的表达式;利用求得的f(an)的表达式代入即可求出
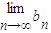 的值;
的值;(3)利用(2)的结论求出bn的表达式,代入
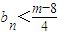 ,整理后把
,整理后把 恒成立问题转化为
恒成立问题转化为 恒成立,最后利用函数的单调性求出
恒成立,最后利用函数的单调性求出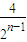 的最值即可求出m的最小值.
的最值即可求出m的最小值.解答:解:(1)
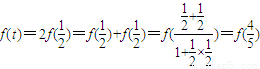 ,
,∴
 (3分)
(3分)(2)∵
 ,且
,且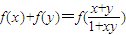
∴
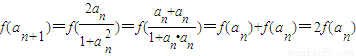 ,
,即
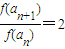
∴f(an)是以-1为首项,2为公比的等比数列,(2分)
∴f(an)=-2n-1.(4分)
∴
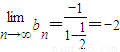 .(8分)
.(8分)(3)由(2)得,
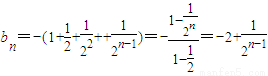 .(1分)
.(1分)若
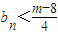 对任意n∈N*恒成立,即
对任意n∈N*恒成立,即 ,
, 恒成立(3分)
恒成立(3分)∵n∈N*,∴当n=1时,
 有最大值4,故m>4.(5分)
有最大值4,故m>4.(5分)又m∈N*,∴存在m≥5,使得对任意n∈N*,有
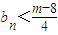 .
.所以mmin=5.(7分)
点评:本题是对数列和函数知识的综合考查.这一类型题,一般都是利用函数的性质来研究数列的性质,做题的关键是把函数的性质理解透彻.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目