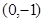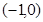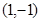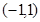题目内容
已知圆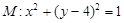 ,直线
,直线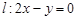 ,点
,点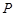 在直线
在直线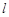 上,过点
上,过点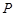 作圆
作圆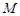 的切线
的切线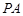 、
、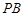 ,切点为
,切点为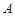 、
、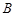 .
.
(Ⅰ)若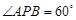 ,求
,求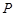 点坐标;
点坐标;
(Ⅱ)若点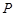 的坐标为
的坐标为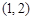 ,过
,过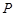 作直线与圆
作直线与圆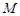 交于
交于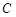 、
、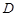 两点,当
两点,当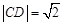 时,求直线
时,求直线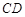 的方程;
的方程;
(III)求证:经过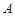 、
、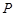 、
、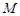 三点的圆与圆
三点的圆与圆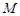 的公共弦必过定点,并求出定点的坐标.
的公共弦必过定点,并求出定点的坐标.
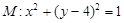 ,直线
,直线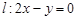 ,点
,点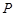 在直线
在直线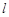 上,过点
上,过点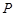 作圆
作圆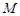 的切线
的切线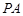 、
、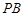 ,切点为
,切点为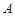 、
、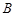 .
.(Ⅰ)若
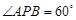 ,求
,求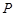 点坐标;
点坐标;(Ⅱ)若点
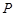 的坐标为
的坐标为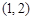 ,过
,过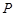 作直线与圆
作直线与圆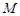 交于
交于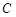 、
、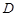 两点,当
两点,当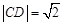 时,求直线
时,求直线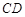 的方程;
的方程;(III)求证:经过
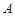 、
、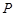 、
、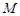 三点的圆与圆
三点的圆与圆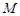 的公共弦必过定点,并求出定点的坐标.
的公共弦必过定点,并求出定点的坐标.(Ⅰ)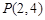 或
或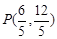 ;(Ⅱ)
;(Ⅱ)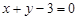 或
或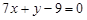 ;(III)
;(III)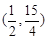
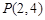 或
或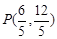 ;(Ⅱ)
;(Ⅱ)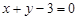 或
或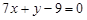 ;(III)
;(III)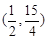
试题分析:解:(Ⅰ)由条件可知
 ,设
,设 ,则
,则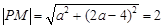 解得
解得 或
或 ,所以
,所以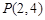 或
或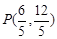 ………………4分
………………4分(Ⅱ)由条件可知圆心到直线
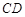 的距离
的距离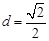 ,设直线
,设直线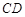 的方程为
的方程为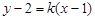 ,
,则
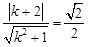 ,解得
,解得 或
或
所以直线
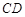 的方程为
的方程为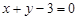 或
或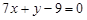 ………………8分
………………8分(III)设
 ,过
,过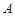 、
、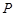 、
、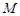 三点的圆即以
三点的圆即以 为直径的圆,
为直径的圆,其方程为
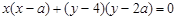
整理得
 与
与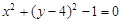 相减得
相减得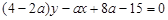
即
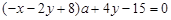
由
 得
得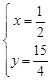
所以两圆的公共弦过定点
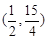 ………………14分
………………14分点评:本题第一、二小题较容易,第三小题较难。但第三小题解法巧妙,使得问题简化。这种解法是这样的,将两圆的方程相减,得到一条直线的方程,由于两圆相交于两点,因而这条直线也经过这两点,故这条直线就是弦所在的直线。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
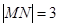 已知椭圆D:
已知椭圆D: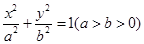 的焦距等于
的焦距等于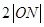 ,且过点
,且过点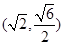

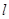 与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补. 的点数共有 个。
的点数共有 个。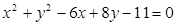 的圆心是( )
的圆心是( )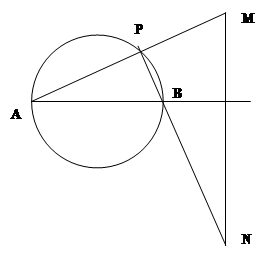
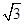 y-4=0相切,
y-4=0相切,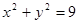 和
和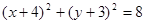 的交点的直线方程
的交点的直线方程  的面积最大时,圆心坐标是 ( )
的面积最大时,圆心坐标是 ( )