题目内容
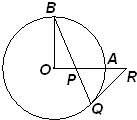
 20、如图,OA和OB是⊙O的半径,并且OA⊥OB,P是线段OA上任意一点,BP的延长线交⊙O于Q,过Q的切线交OA的延长线于R,则RP、RQ的大小关系是
20、如图,OA和OB是⊙O的半径,并且OA⊥OB,P是线段OA上任意一点,BP的延长线交⊙O于Q,过Q的切线交OA的延长线于R,则RP、RQ的大小关系是RP=RQ
.分析:连接OQ,易得△OBQ为等腰三角形,由切线的性质,可得OQ⊥QR,则由等腰的余角相等及对顶角相等,可得∠QPR=∠BQR,即△RPQ为等腰三角形,进而判断出RP、RQ的大小关系.
解答:解:连接OQ,如下图所示:

∵OQ=OB
∴∠OQB=∠OBQ
∵PQ为圆O的切线,OA⊥OB
∴∠BPO=90°-∠OBQ,∠BQR=90°-∠OQB
∴∠BPO=∠QPR=∠BQR,
即△RPQ为等腰三角形
∴RP=RQ
故答案为:RP=RQ

∵OQ=OB
∴∠OQB=∠OBQ
∵PQ为圆O的切线,OA⊥OB
∴∠BPO=90°-∠OBQ,∠BQR=90°-∠OQB
∴∠BPO=∠QPR=∠BQR,
即△RPQ为等腰三角形
∴RP=RQ
故答案为:RP=RQ
点评:本题考查的知识点是切线的性质,等腰三角形的判定与性质,其中添加辅助线,以帮助分析题目中角与解之间的关系,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•河西区一模)如图,OA和OB是⊙O的半径,且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,过作⊙O的切线交OA延长线于R,RP2,则RQ=
(2012•河西区一模)如图,OA和OB是⊙O的半径,且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,过作⊙O的切线交OA延长线于R,RP2,则RQ=