题目内容
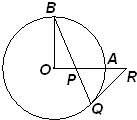
如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,过Q作⊙O的切线交OA的延长线于R,求证:RP=RQ.

答案:
解析:
提示:
解析:
|
证明:连结OQ. 因为QR是⊙O的切线, 所以OQ⊥QR. 因为OB=OQ, 所以∠B=∠OQB. 因为BO⊥OA, 所以∠BPO=90°-∠B=∠RPQ, ∠PQR=90°-∠OQP. 所以∠RPQ=∠PQR. 所以RP=RQ. 分析:已知QR是⊙O的切线,可利用切线的性质定理,即OQ⊥RQ.另外,要证RP=RQ,只要证∠RPQ=∠RQP即可,只要证∠BPO=∠PQR即可,再结合OQ⊥RQ. |
提示:
|
题目中若有圆的切线,首先可以连结圆心和切点,出现垂直关系. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 20、如图,OA和OB是⊙O的半径,并且OA⊥OB,P是线段OA上任意一点,BP的延长线交⊙O于Q,过Q的切线交OA的延长线于R,则RP、RQ的大小关系是
20、如图,OA和OB是⊙O的半径,并且OA⊥OB,P是线段OA上任意一点,BP的延长线交⊙O于Q,过Q的切线交OA的延长线于R,则RP、RQ的大小关系是 (2012•河西区一模)如图,OA和OB是⊙O的半径,且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,过作⊙O的切线交OA延长线于R,RP2,则RQ=
(2012•河西区一模)如图,OA和OB是⊙O的半径,且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,过作⊙O的切线交OA延长线于R,RP2,则RQ=