题目内容
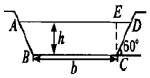
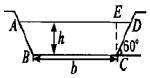
一条水渠的断面为等腰梯形(如图所示),在确定断面尺寸时,希望在断面ABCD的面积为定值S时,使得湿周l=AB+BC+CD最小且这样可使水流阻力小且渗透少,求此时的高h和下底边长b.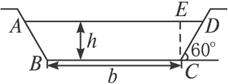
解:由梯形面积公式,得S=![]() (AD+BC)h,
(AD+BC)h,
其中AD=2DE+BC,DE=![]() h,BC=b.
h,BC=b.
∴AD=![]() h+b.
h+b.
∴S=![]() (
(![]() h+2b)h=(
h+2b)h=(![]() h+b)h. ①
h+b)h. ①
∵CD=![]() h,AB=CD,
h,AB=CD,
∴l=![]() h×2+b. ②
h×2+b. ②
由①得b=![]() ,代入②,
,代入②,
∴l=![]() h+
h+![]() h=
h=![]() h+
h+![]() .
.
∵l′=![]() -
-![]() =0,∴h=
=0,∴h=![]() .
.
当h<![]() 时,l′<0;当h>
时,l′<0;当h>![]() 时,l′>0.
时,l′>0.
∴当h=![]() 时,l取最小值,此时b=
时,l取最小值,此时b=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目