题目内容
已知a=
，b=
，c=
，则a，b，c大小关系为________．
c＞b＞a
分析：由对数式的运算性质得到a＜0，由幂函数的单调性得到c＞b＞0，所以答案可求．
解答：∵
，
又∵函数y=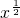
在（0，+∞）是增函数，
∴
＞0．
所以，c＞b＞a．
故答案为c＞b＞a．
点评：本题考查了对数式的运算性质，考查了幂函数的性质，是基础的不等式大小比较问题．
分析：由对数式的运算性质得到a＜0，由幂函数的单调性得到c＞b＞0，所以答案可求．
解答：∵
，又∵函数y=
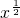在（0，+∞）是增函数，∴
＞0．所以，c＞b＞a．
故答案为c＞b＞a．
点评：本题考查了对数式的运算性质，考查了幂函数的性质，是基础的不等式大小比较问题．
练习册系列答案
相关题目
已知A、B、C是锐角△ABC的三个内角，向量
=(-sinA，1)
=(1，cosB)，则
与
的夹角是（ ）
| p |
| q |
| p |
| q |
| A、锐角 | B、钝角 | C、直角 | D、不确定 |