题目内容
已知函数f(x)=2sinωxcosωx+2 sin2ωx-
sin2ωx- (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求函数f(x)的单调增区间;
(2)将函数f(x)的图象向左平移 个单位,再向上平移1个单位长度,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位长度,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
解 (1)由题意得:f(x)
=2sinωxcosωx+2 sin2ωx-
sin2ωx-
=sin2ωx- cos2ωx=2sin
cos2ωx=2sin ,
,
由最小正周期为π,得ω=1.
 整理得
整理得 k∈Z,所以函数f(x)的单调增区间是
k∈Z,所以函数f(x)的单调增区间是
(2)将函数f(x)的图象向左平移 个单位长度,再向上平移1个单位长度,得到y=2sin2x+1的图象,所以g(x)=2sin2x+1.
个单位长度,再向上平移1个单位长度,得到y=2sin2x+1的图象,所以g(x)=2sin2x+1.
令g(x)=0,得 所以y=g(x)在[0,π]上恰好有两个零点.若y=g(x)在[0,b]上至少有10个零点,则b不小于第10个零点的横坐标即可,即b的最小值为
所以y=g(x)在[0,π]上恰好有两个零点.若y=g(x)在[0,b]上至少有10个零点,则b不小于第10个零点的横坐标即可,即b的最小值为

练习册系列答案
相关题目
 .其中符号为负的是( )
.其中符号为负的是( ) B.y=cos
B.y=cos
 D.y=cos
D.y=cos 图象上所有点的横坐标缩短到原来的
图象上所有点的横坐标缩短到原来的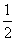 (纵坐标不变),再把所得图象向右平移
(纵坐标不变),再把所得图象向右平移 个单位长度后得到函数y=f(x)的图象,则函数y=f(x)的图象( )
个单位长度后得到函数y=f(x)的图象,则函数y=f(x)的图象( ) 对称C.关于直线x=
对称C.关于直线x= 对称 D.关于直线x=π对称
对称 D.关于直线x=π对称 (1)求实验室这一天的最大温差;
(1)求实验室这一天的最大温差;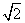 +1,且sinA+sinB=
+1,且sinA+sinB=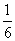 sinC,则角C的大小为( )
sinC,则角C的大小为( ) ,则
,则 的最大值为( )
的最大值为( ) B.
B.
 sinB=2sinC,则cosC的最小值是________.
sinB=2sinC,则cosC的最小值是________. ,
, =120.
=120.
 求x,y的值.
求x,y的值.