Question

8．若点P（m，3）到直线4x-3y+1=0的距离为5，且点P在不等式2x+y＜3表示的平面区域内，则m=（　　）

• A． $-\frac{15}{4}$
• B． $-\frac{17}{4}$
• C． $\frac{33}{4}$
• D． $-\frac{17}{4}$或$\frac{33}{4}$

Answer 1

分析 利用点到直线的距离公式列出关系式，把已知距离代入求出m的值，根据点P在不等式2x+y＜3表示的平面区域内判断即可．

解答 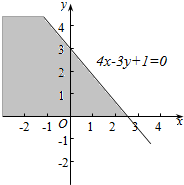解：∵点P（m，3）到直线4x-3y+1=0的距离为5，
∴$\frac{|4m-9+1|}{\sqrt{{4}^{2}+（-3）^{2}}}$=5，即|4m-8|=25，
解得：m=-$\frac{17}{4}$或m=$\frac{33}{4}$，
∵点P在不等式2x+y＜3表示的平面区域内，
∴m=$\frac{33}{4}$不合题意舍去，
则m=-$\frac{17}{4}$，
故选：B．

点评 此题考查了二元一次不等式（组）与平面区域，利用了数形结合的思想，画出相应的图形是解本题的关键．