题目内容
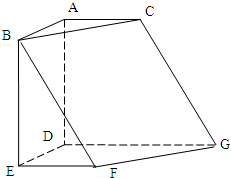 (2010•天津模拟)如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AB=AD=DE=DG=2,AC=EF=1.
(2010•天津模拟)如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AB=AD=DE=DG=2,AC=EF=1.(Ⅰ)求证:BF∥平面ACGD;
(Ⅱ)求二面角A-EG-D的正切值;
(Ⅲ) 求六面体ABCDEFG的体积.
分析:(Ⅰ)设DG的中点为M,连接AM、FM,证明BF平行平面ACGD内的直线AM,即可证明BF∥平面ACGD;
(Ⅱ)连接EG,取EG的中点O,连接DO,AO,则易得∠AOD为所求二面角的平面角,从而可求二面角A-EG-D的正切值;
(Ⅲ)利用V多面体ABC-DEFG=V三棱柱ADM-BEF+V三棱柱ABC-MFG直接求五面体ABCDEFG的体积.
(Ⅱ)连接EG,取EG的中点O,连接DO,AO,则易得∠AOD为所求二面角的平面角,从而可求二面角A-EG-D的正切值;
(Ⅲ)利用V多面体ABC-DEFG=V三棱柱ADM-BEF+V三棱柱ABC-MFG直接求五面体ABCDEFG的体积.
解答:证明:(Ⅰ)设DG的中点为M,连接AM、FM,
则由已知条件易证四边形DEFM是平行四边形,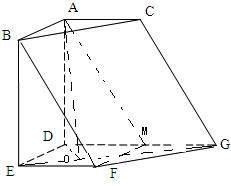
所以MF∥DE,且MF=DE
又∵AB∥DE,且AB=DE
∴MF∥AB,且MF=AB
∴四边形ABMF是平行四边形,即BF∥AM,
又BF?平面ACGD 故BF∥平面ACGD
(Ⅱ)连接EG,取EG的中点O,连接DO,AO
∵DE=DG=2,∴DO⊥EG,DO=
∵AD⊥平面DEFG,∴AO⊥EG
∴∠AOD为所求二面角的平面角
∵AD=2,∴tan∠AOD=
=
∴二面角A-EG-D的正切值为
(Ⅲ)V多面体ABC-DEFG=V三棱柱ADM-BEF+V三棱柱ABC-MFG=DE×S△ADM+AD×S△MFG
=2×
×2×1+2×
×2×1=4.
则由已知条件易证四边形DEFM是平行四边形,

所以MF∥DE,且MF=DE
又∵AB∥DE,且AB=DE
∴MF∥AB,且MF=AB
∴四边形ABMF是平行四边形,即BF∥AM,
又BF?平面ACGD 故BF∥平面ACGD
(Ⅱ)连接EG,取EG的中点O,连接DO,AO
∵DE=DG=2,∴DO⊥EG,DO=
| 2 |
∵AD⊥平面DEFG,∴AO⊥EG
∴∠AOD为所求二面角的平面角
∵AD=2,∴tan∠AOD=
| 2 | ||
|
| 2 |
∴二面角A-EG-D的正切值为
| 2 |
(Ⅲ)V多面体ABC-DEFG=V三棱柱ADM-BEF+V三棱柱ABC-MFG=DE×S△ADM+AD×S△MFG
=2×
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查直线与平面平行的判定,棱柱、棱锥、棱台的体积,考查逻辑思维能力,空间想象能力,考查面面角,关键是根据题意作出二面角的平面角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 (2010•天津模拟)某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是
(2010•天津模拟)某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是