题目内容
在△ABC中,a,b,c分别为角A,B,C所对的边,且4sin2
-cos2A=
.(参考公式:sin2
=
,cos2α=2cos2α-1)
(1)求角A的度数;
(2)若a=
,b+c=3,求b和c的值.
| B+C |
| 2 |
| 7 |
| 2 |
| α |
| 2 |
| 1-cosα |
| 2 |
(1)求角A的度数;
(2)若a=
| 3 |
(1)由题设得2[1-cos(B+C)]-(2cos2A-1)=
,
∵cos(B+C)=-cosA,
∴2(1+cosA)-2cos2A+1=
,
整理得(2cosA-1)2=0,
∴cosA=
,
∴A=60°;
(2)∵cosA=
=
=
=
=
,
∴bc=2,
又∵b+c=3,
∴b=1,c=2或b=2,c=1.
| 7 |
| 2 |
∵cos(B+C)=-cosA,
∴2(1+cosA)-2cos2A+1=
| 7 |
| 2 |
整理得(2cosA-1)2=0,
∴cosA=
| 1 |
| 2 |
∴A=60°;
(2)∵cosA=
| b2+c2-a2 |
| 2bc |
| (b+c)2-2bc-a2 |
| 2bc |
| 9-2bc-3 |
| 2bc |
| 6-2bc |
| 2bc |
| 1 |
| 2 |
∴bc=2,
又∵b+c=3,
∴b=1,c=2或b=2,c=1.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
 的公差
的公差 ,且
,且 成等比数列,则
成等比数列,则 的值是( )
的值是( )



 中,前
中,前 项和
项和 ,若
,若 ,
, ,则
,则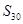 = .
= .