题目内容

5．若一个正三棱柱（底面为正三角形，侧面为矩形的棱柱）的三视图如图所示，则这个正三棱柱的侧棱长和底面边长分别为2，4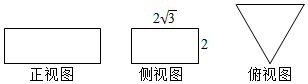

分析 由俯视图可知三棱柱高为2，底面三角形的高为2$\sqrt{3}$．

解答 解：由侧视图可知三棱柱的高为2，即侧棱长为2．
由侧视图可得底面正三角形的高为2$\sqrt{3}$，
∴底面正三角形的边长为4．
故答案为：2，4．

点评 本题考查了棱柱的三视图和结构特征，属于基础题．

练习册系列答案
相关题目
17．在长方体ABCD-A1B1C1D1中，AB=3，BC=2，AA1=1，点M，N，P分别是棱AB，BC，CC1的中点，则三棱锥C1-MNP的体积为$\frac{1}{8}$．
17．执行如图所示的程序框图，则输出的S等于（　　）
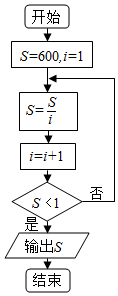
A．$\frac{1}{2}$B．$\frac{3}{5}$C．$\frac{5}{6}$D．$\frac{6}{7}$
14．已知数列{an}的前n项和为Sn，且3Sn+an-3=0，n∈N*．
（1）求数列{an}的通项公式；
（2）设数列{bn}满足bn=$\frac{1}{2}{log_2}（{1-{S_{n+1}}}）$，求Tn=$\frac{1}{{{b_1}{b_2}}}+\frac{1}{{{b_2}{b_3}}}+…+\frac{1}{{{b_n}{b_{n+1}}}}$，求使Tn≥$\frac{504}{1009}$成立的n的最小值．
1．若三棱柱ABC-A1B1C1的体积为V，P为CC1上的一点，${V}_{P-AB{B}_{1}{A}_{1}}$=$\frac{2V}{3}$．
10．${（x-\frac{1}{{\sqrt{x}}}）^6}（2{x^3}+1）$的常数项是（　　）
A．15B．17C．-15D．-17
17．已知等差数列{an}的前n项和为Sn，满足S4=4（a3+1），3a3=5a4．
（1）求数列{an}的通项公式；
（2）求数列{|an|}的前n项和为Tn．
14．由曲线y=$\sqrt{x}$，直线y=x所围成的封闭曲线的面积是（　　）
A．$\frac{1}{6}$B．$\frac{1}{2}$C．$\frac{2}{3}$D．1
14．F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点．过点F向C的-条渐近线引垂线，垂足为A，交另一条渐近线于点B，若3$\overrightarrow{AF}$=$\overrightarrow{FB}$，则C的心离心率是（　　）
A．$\sqrt{2}$B．2C．$\frac{\sqrt{6}}{2}$D．$\frac{\sqrt{14}}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网