题目内容
1.判断圆x2+y2-2x-3=0和x2+y2-4y+3=0的位置关系.分析 把两圆的方程化为标准方程,分别找出圆心坐标和半径,利用两点间的距离公式,求出两圆心的距离d,然后求出R-r和R+r的值,判断d与R-r及R+r的大小关系即可得到两圆的位置关系.
解答 解:把圆x2+y2-2x-3=0和x2+y2-4y+3=0分别化为标准方程得:
(x-1)2+y2=4,x2+(y-2)2=1,
故圆心坐标分别为(1,0)和(0,2),半径分别为R=2和r=1,
∵圆心之间的距离d=$\sqrt{5}$,R+r=3,R-r=1
∴R-r<d<R+r,
则两圆的位置关系是相交.
点评 本题考查圆与圆的位置关系,位置关系分别是:当0≤d<R-r时,两圆内含;当d=R-r时,两圆内切;当R-r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R+r时,两圆外离(其中d表示两圆心间的距离,R,r分别表示两圆的半径).

练习册系列答案
相关题目
9.若x,y满足$\left\{\begin{array}{l}x+y≤4\\ x-2y≥0\\ x+2y≥4\end{array}\right.$,则$z=\frac{y-4}{x-3}$的取值范围是( )
| A. | (-∞,-4]∪[3,+∞) | B. | (-∞,-2]∪[-1,+∞) | C. | [-2,-1] | D. | [-4,3] |
16.已知角α的终边经过点P(4,-3),则sinα+2cosα的值等于( )
| A. | $-\frac{3}{5}$ | B. | $-\frac{2}{5}$ | C. | 1 | D. | $\frac{4}{5}$ |
13.下列函数没有零点的是( )
| A. | $f(x)={log_2}^x-3$ | B. | $f(x)=\sqrt{x}-4$ | C. | f(x)=$\frac{1}{x-1}$ | D. | f(x)=x2+2x |
10.圆C:x2+y2-4=0被直线l:x-y+2=0截得的弦长为( )
| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $4\sqrt{2}$ |
 对a、b∈R,记$max\left\{{a\;,\;\;b}\right\}=\left\{\begin{array}{l}a\;,\;\;a≥b\\ b\;,\;\;a<b\end{array}\right.$,函数f(x)=max{|x|,-x2-2x+2},x∈(-4,3)
对a、b∈R,记$max\left\{{a\;,\;\;b}\right\}=\left\{\begin{array}{l}a\;,\;\;a≥b\\ b\;,\;\;a<b\end{array}\right.$,函数f(x)=max{|x|,-x2-2x+2},x∈(-4,3)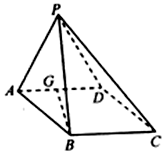 如图所示,在四棱锥P-ABCD中,G为AD的中点,侧面PAD⊥底面ABCD.底面ABCD是边长为a的菱形,且∠D A B=60°,侧面PAD为正三角形.求证:AD⊥平面PGB.
如图所示,在四棱锥P-ABCD中,G为AD的中点,侧面PAD⊥底面ABCD.底面ABCD是边长为a的菱形,且∠D A B=60°,侧面PAD为正三角形.求证:AD⊥平面PGB.